P3941 Ruzhenqu

PDF statement and large samples link: http://pan.baidu.com/s/1cawM7c Password: xgxv. ```plain 丹青千秋酿，一醉解愁肠。 无悔少年枉，只愿壮志狂。 ```

Xiao F likes mathematics very much, but after entering high school he has never done well in math exams. One day, he spaced out during math class; he thought about the past year. A year ago, when he first encountered algorithm contests, he felt that the whole world was brand new. How could there be so many wonderful things in this world? Problems that he used to think were hard were easily solved by one algorithm after another. Back then, Xiao F secretly felt that, compared with his own naivety, he still had a lot to learn. A year has passed, and thinking about it still feels a bit unreal. He can still remember that one night, listening to Ruzhenqu, he was too excited to sleep. He kept solving problems until the rooster crowed at dawn, and he was still thrilled. Maybe that’s what “hot-blooded” feels like.  It was around that time that Xiao F learned matrix multiplication. Multiplying two matrices a few times to compute the $10^{100}$-th term of the Fibonacci sequence felt truly amazing. However, Xiao F does not want to do matrix multiplication by hand now—he finds it troublesome. Instead, he came up with a simple little problem. He drew an $n \times m$ matrix, with each cell containing a positive integer not exceeding $k$. Xiao F wants to ask you: how many different subrectangles in this matrix have a sum of numbers that is a multiple of $k$? If a subrectangle is described by its top-left and bottom-right corners as $(x_1,y_1,x_2,y_2)$, where $x_1 \le x_2, y_1 \le y_2$; then we consider two subrectangles to be different if and only if their $(x_1,y_1,x_2,y_2)$ representations differ. In other words, as long as two rectangles have the same $(x_1,y_1,x_2,y_2)$ representation, they are regarded as the same rectangle, and you should count it only once in your answer.

Read from standard input. The first line contains three positive integers $n,m,k$. The next $n$ lines each contain $m$ positive integers. In the $i$-th row, the $j$-th column contains the positive integer $a_{i,j}$.

Output to standard output. Output a single non-negative integer on one line, which is your answer.

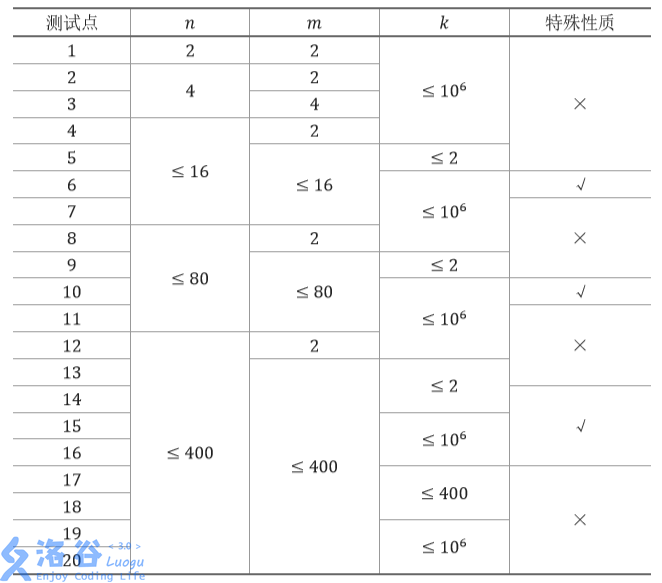
[Sample 1 explanation] These rectangles meet the requirement: $(1, 1, 1, 3),(1, 1, 2, 2),(1, 2, 1, 2),(1, 2, 2, 3),(2, 1, 2, 1),(2, 3, 2, 3)$. Subtasks will provide characteristics of some testdata. If you find the problem difficult, you can try solving only part of the testdata. The data scale and characteristics for each test point are shown in the following table:  Special property: all $a_{i,j}$ are guaranteed to be equal. Translated by ChatGPT 5