P3942 General's Order

> History/falls into/the victor's/hands > At least/we/have/legends > Who says/the defeated/cannot/be immortal > Fists/can only/make people/bow their heads > Thoughts/can/make people/lift their heads > Lift your head/to look/to love/to chase > The dream in your heart.

April comes to mind again. If not for the NOI Qualifier, we probably wouldn’t have parted ways so easily, right? One by one, former teammates left the computer room. “Speak no more of marquisates; a general's success is built upon myriad bones.” In a dream, little F became a courier delivering secret letters to a general. Now, there are two secret letters crucial to the life and death of the nation that must be delivered to the commanding general at the front. The journey is perilous and time is tight. Little F, undeterred by personal risk, bravely takes on the task. However, little F is very careless. He accidentally lost one of the two secret letters. He secretly opened the remaining letter and found a very detailed map together with a few annotations—turns out it was an intelligence map of the battlefield and its surroundings. On this map, there are $n$ relay stations labeled from $1$ to $n$, and $n - 1$ small roads of length $1$ li, each road bidirectionally connecting two different relay stations. Any two stations are reachable via these roads. Carefully reading the notes, little F suddenly understood the contents of the lost letter. Each relay station can host one squad, and each squad can control all stations within a distance no more than $k$ li. If any station is left uncontrolled, danger may arise—so such situations must be completely avoided. The lost secret letter contained a brilliant arrangement from the imperial mathematical minister: an optimal placement using the fewest squads to control all relay stations. Little F knows that if he can compute the optimal plan, he might redeem his mistake and avoid the death penalty. He found you—can you help him? Of course, while waiting for your assistance, little F may have observed some potentially useful properties from the map, which he will convey to you in a special way.

Read from standard input. The first line contains three positive integers $n$, $k$, $t$, representing the number of relay stations, the maximum distance a squad can control, and the code for a special property. For the special property, see the Hint. The next $n - 1$ lines each contain two positive integers $u_i$, $v_i$, indicating that there is a bidirectional small road of length $1$ li between $u_i$ and $v_i$.

Write to standard output. Output a single line: the number of squads required under an optimal plan.

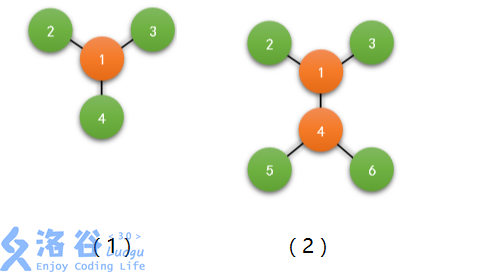
[Sample 1 Explanation] As shown in the figure. Since the distance from node $1$ to its surrounding nodes is $1$, it can control all relay stations. [Sample 2 Explanation] As shown in the figure, similar to Sample 1.  Subtasks will provide some characteristics of the testdata. If you find the problem difficult, you can try to solve only part of the testdata. The meaning of $t$ is as follows: - $t = 0$: This test point has no additional special property. - $t = 1$: It is guaranteed that at most $8$ nodes are incident to more than $1$ road. - $t = 2$: It is guaranteed that the distance from every node to node $1$ is at most $2$. 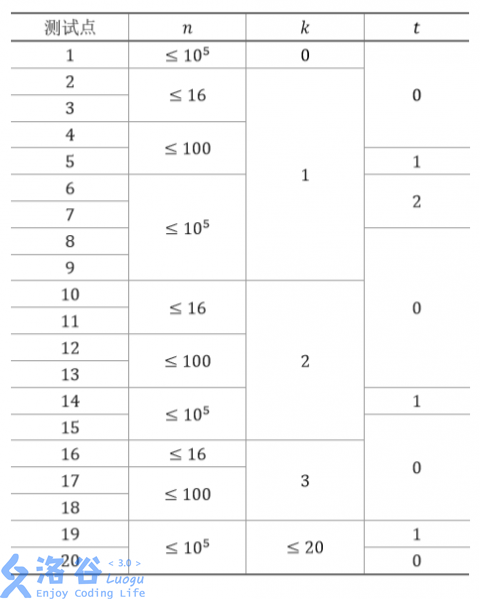The scale and characteristics of each test point are shown in the following table:  Translated by ChatGPT 5