P3946 Kotori's Snack

It is the winter of 2017. (It is the season of White Album again 2333.)  After skiing, Kotori suddenly wants a snack, so she goes to a dessert shop. It often snows in winter in Japan. Unfortunately, today is the same, and the snow depth increases by $q$ millimeters every second. Akihabara has $n$ locations, numbered from $1$ to $n$. Each location initially has a snow depth of $h_i$. There are $m$ bidirectional roads connecting these locations, and their lengths are $w_i$ meters. The snow is too heavy and public transportation has stopped, so Kotori has to walk home. Her walking speed is $1$ m/s. For convenient mapping, the road network ensures that each road strictly connects two different locations, and there are no two roads connecting the same pair of locations. Each location has a limit snow height $l_i$ in millimeters. If, upon arrival, the snow depth there is greater than $l_i$, she will be trapped at that location and cannot leave, and thus cannot reach Kotori's home. The dessert shop is location $s$, and Kotori's home is location $t$. Do not consider the snow at the dessert shop and at Kotori's home. Kotori wants to get home within $g$ seconds, as fast as possible. If she cannot reach home within $g$ seconds, or she gets trapped on the way, then she will turn wtnap into her snack ( ・ 8 ・ ).

The first line contains $6$ integers, separated by spaces: $n$, $m$, $s$, $t$, $g$, $q$. The next $n$ lines each contain $2$ integers, separated by spaces, representing $h_i$ and $l_i$ for that location. The next $m$ lines each contain $3$ integers, separated by spaces, representing the two locations $u$, $v$ connected by the road and the road length $w_i$.

Output one line with one integer, the shortest time to reach Kotori's home. If wtnap becomes Kotori's snack, output "wtnap wa kotori no oyatsu desu!" without quotes.

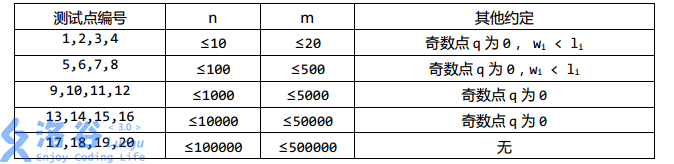
For $0\%$ of the testdata, the same as the sample. For $40\%$ of the testdata, $q = 0$. For $50\%$ of the testdata in the previous line, all $w_i < l_i$. For $100\%$ of the testdata, $1 \le s, t \le n$; $0 \le g, q \le 10^9$; $0 \le w_i \le l_i \le 10^9$.  Translated by ChatGPT 5