P3948 Data Structures

Introduction If you learn data structures well, your future job will have no worries. Edgration (hereafter edt) is a "ju ruo" (newbie) who likes to mess with data structures. One day, he decided to make things hard for some "dalao" (experts): edt: I want a data structure that supports range add and can return the number of elements greater than $k$ in a given interval. dalao1: sb segment tree. dalao2: sb block decomposition. dalao3: sb balanced tree. edt: Not good enough, then add modulo: count, after taking modulo, how many numbers in the interval are greater than MIN and less than MAX. dalao1: segment tree &……￥#&……%……&\*&%￥. dalao2: sb block decomposition &%￥……%#￥#&……&\*. dalao3: *&……%&￥ LCT maintaining SBT easy problem &……%&……%. edt: Not only modulo, but also multiply each number by its array index and then take modulo. dalao: ￥%￥￥&*（#￥% gibberish gibberish. edt: No, then throw the modulo values onto a tree and maintain the minimum range of the cactus product variance. dalao: Use scapegoat tree with sb block linked list to maintain min-cost max-flow on Toptree and a persistent cactus, then invert in the Kirchhoff matrix and run plug DP maintained by fft. Give me three minutes, easy pass. edt: mmp.

The newbie edt gives this problem to you—a master of data structures. Since this is the first problem, it is not that hard.  The problem is simplified as follows: - Initially, every element in the array is $0$. - You are given $\text{n}, \text{opt}, \text{mod}, \text{min}, \text{max}$ within the range of `int`. Operations $A, Q$: - `A L R X` means add $X$ to the interval $[L, R]$. (Every element from $L$ to $R$ in the array is increased by $X$.) - `Q L R` asks, in the interval $[L, R]$, for the count of elements $T$ such that $\text{min} \le (T \times i \mod \text{mod}) \le \text{max}$, where $i$ is the array index. (The value of the element times its index, modulo $\text{mod}$, falls within the range from $\min$ to $\max$, inclusive.) Because edt invited a non-3D hamster to help, some queries are postponed into a chaotic spacetime. The number of online `Q` operations will not exceed $1000$. Unfortunately, there may be many postponed queries (less than $1 \times 10^7$), but it is guaranteed that after these postponed queries, there will be no more update operations (that is, at the end there are many queries but no modifications).

- The first line gives $\text{n}, \text{opt}, \text{mod}, \text{min}, \text{max}$, representing the sequence size, the number of operations, the modulo, the minimum value, and the maximum value. - Then follow $\text{opt}$ lines, each being one of: - `A L R X` denotes a range add. $\text{X}$ is guaranteed to be within the range of `int`. - `Q L R` denotes a range query asking for the count that satisfies the condition. - The $(\text{opt} + 1)$-th line gives a number $\text{Final}$, meaning there are $\text{Final}$ postponed queries after that. - Then follow $\text{Final}$ lines, each giving $L, R$, asking for the count that satisfies the condition in $[L, R]$.

- For each `Q` operation, output one number per line representing the answer to that query. - Then output $\text{Final}$ lines, each with one number representing the answer to each postponed query.

Sample Explanation Explanation for Sample 1: In Sample 1, the array $a$ becomes $5, 5, 5$. Each $a_i \times i \mod 4$ equals $1, 2, 3$. For the $\text{Final}$ queries, in $[1, 3]$, the count of values greater than or equal to $0$ and less than or equal to $2$ is $2$. The rest are similar. Notes - Important: - Regarding modulo with negative numbers, follow C++ truncation toward $0$. For example: [ $ -7 \bmod 3 = -1 $ ] [ $ 7 \bmod 3 = 1 $ ]. - There are 50 test points, each worth 2 points. Because there are many test points, please do not intentionally submit many times to jam the judge. The author edt expresses sincere thanks. 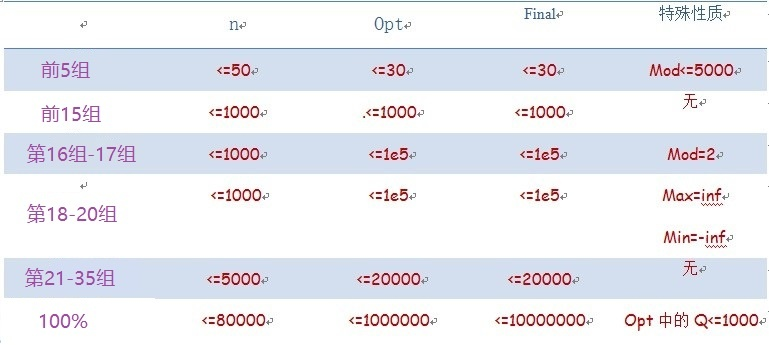Constraints If you cannot solve all points, try to obtain partial scores. All testdata are randomly generated.  Translated by ChatGPT 5