P3948 数据结构
题目背景
**引言**
数据结构学的好，未来工作没烦恼。
Edgration 是一个喜欢乱搞数据结构的蒟蒻（以下简称edt），有一天，他作死想去刁难一下 dalao：
edt 想求一种数据结构，使得可以实现区间加，求出某一区间大于 $k$ 的元素的个数。
dalao1：sb 线段树。
dalao2：sb 分块。
dalao3：sb 平衡树。
edt: 不行，那就加上取模，求区间取膜 mod 后大于 MIN 小于 MAX 的元素个数。
dalao1：线段树&……￥#&……%……&\*&%￥。
dalao2：sb 分块 &%￥……%#￥#&……&\*。
dalao3：*&……%&￥ LCT 维护 SBT 水题 &……%&……%。
edt：那不仅取模，每个数乘上数组下标再取模。
dalao：￥%￥￥&*（#￥% 叽里呱啦叽里呱啦。
edt：不行，在把取模的值丢到一棵树上，维护一棵仙人掌乘积方差的最小极差。
dalao：替罪羊树上用 sb 块状链表维护 Toptree 上的最小费用最大流和可持久化仙人掌，算出来在基尔霍夫矩阵中反演后跑一遍 fft 维护的插头 DP 就好了，给我三分钟轻松水过。
edt：mmp。
题目描述
蒟蒻 Edt 把这个问题交给了你—— 一个精通数据结构的大犇，由于是第一题，这个题没那么难。
edt 现在对于题目进行了如下的简化：
最开始的数组每个元素都是 $0$。
给出 $\text{n},\text{opt},\text{mod},\text{min},\text{max}$ 在 `int` 范围内。
操作 $A,Q$：
`A L R X` 表示把 $[L,R]$ 这个区间加上 $X$。
**（数组的从 $L$ 到 $R$ 的每个元素都加上 $X$）**
`Q L R` 表示询问 $[L,R]$ 这个区间中元素 $T$ 满足 $\text{min}\le (T\times i\ mod\ \text{mod})\le \text{max}$ 的 $T$ 这样的数的个数（$i$ 是数组下标）。
**（元素的值 $\times$ 数组下标对 $\text{mod}$ 取模的值在 $\min$ 到 $\max$ 范围内）**
由于 edt 请来了一位非三次元的仓鼠，他帮你用延后了部分问题，将这些询问打入了混乱时空，你的询问操作不会超过 $1000$ 次，不幸的是，对于延后的询问操作可能有很多次（小于 $1\times10^7$ 次），但是保证这些延后的询问操作之后不会再次有修改操作（就是在最后会有很多次询问，但不会进行修改）。
输入格式
给出 $\text{n},\text{opt},\text{mod},\text{min},\text{max}$ 分别表示序列大小，操作次数，取膜，最小值，最大值。
下面 $\text{opt}$ 行，给出：
`A L R X` 表示区间加，保证 $\text{X}$ 在 `int` 范围内（$X
输出格式
每行对于每个 $Q$ 操作输出 $Q$ 个数表示每次询问的值，
下面 $\text{Final}$ 行表示 $\text{Final}$ 个询问的值。
说明/提示
## 样例说明
给出样例 1 的解释：
样例 1 中，$a$ 数组修改为$5,5,5$，每个 $a_i\times i\ mod\ 4$ 的值为 $1,2,3$。
对于 $\text{Final}$ 的询问，询问 $[1,3]$ 中大于等于 $0$ 小于等于 $2$ 的个数为 $2$ 个。
剩下的询问类似。
## 题目说明
**注意**：
### 1.关于负数取模问题，请以 c++ 的向 $0$ 取整为标准，即如：
[ $ -7 \bmod 3 = -1 $ ] [ $ 7 \bmod 3 = 1 $ ]
### 2.一共会有 50 个测试点，每个点分值为 2 分。
因为测试点数较多，请 OIer 们自觉地不要故意多次提交来卡评测机，出题人 edt 在这里表示由衷的感谢。
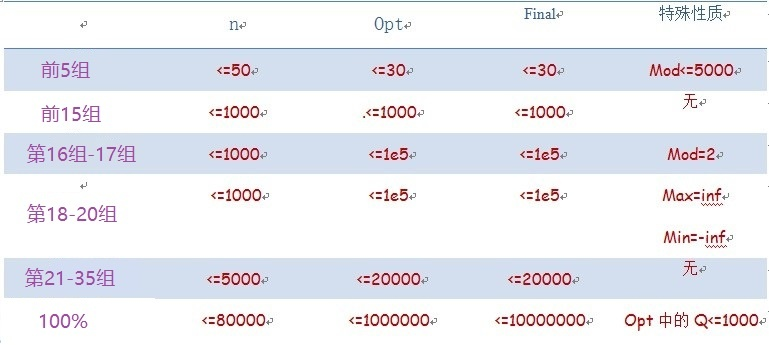
## 数据范围
如果你不能做对所有点，请尝试获得部分分，所有数据都是随机生成。
