P3959 [NOIP 2017 Senior] Treasure

NOIP 2017 D2T2.

Xiaoming, who is taking part in an archaeological dig, obtained a treasure map. The map marks $n$ treasure chambers buried deep underground, and gives $m$ developable roads between these $n$ chambers together with their lengths. Xiaoming resolves to excavate the treasure in all chambers. However, every chamber is far from the surface. That is, opening a road from the surface to some chamber is difficult, whereas opening roads between chambers is much easier. Moved by Xiaoming’s determination, the sponsor decides to open for free exactly one passage from the surface to a chamber, and Xiaoming can choose which chamber it leads to. After that, Xiaoming must decide how to open roads between chambers. Any already opened road can be traversed arbitrarily at no cost. Each time a new road is opened, Xiaoming and the team excavate the treasure chambers that become reachable via that road. Moreover, Xiaoming does not want to open useless roads; that is, a road between two already excavated chambers need not be opened. The cost to open a new road is $L \times K$, where $L$ is the road’s length, and $K$ is the number of chambers along the path from the sponsored chamber to the starting chamber of this road (including both the sponsored chamber and this road’s starting chamber). Choose the sponsored chamber and the subsequent roads to open so that the total cost is minimized, and output this minimum.

The first line contains two space-separated positive integers $n,m$, the number of treasure chambers and the number of roads. The next $m$ lines each contain three space-separated positive integers: the indices of two chambers connected by a road (numbered $1-n$), and the length $v$ of that road.

Output a single positive integer, the minimum total cost.

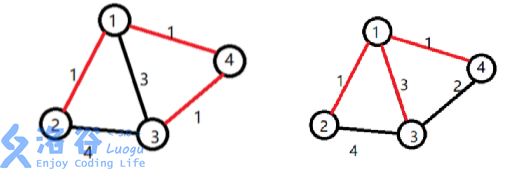
 [Sample explanation $1$] Xiaoming chooses chamber $1$ to be opened by the sponsor. Xiaoming opens road $1 \to 2$ and excavates chamber $2$. He opens road $1 \to 4$ and excavates chamber $4$. He also opens road $4 \to 3$ and excavates chamber $3$. The total cost is $1 \times 1 + 1 \times 1 + 1 \times 2 = 4$. [Sample explanation $2$] Xiaoming chooses chamber $1$ to be opened by the sponsor. Xiaoming opens road $1 \to 2$ and excavates chamber $2$. He opens road $1 \to 3$ and excavates chamber $3$. He also opens road $1 \to 4$ and excavates chamber $4$. The total cost is $1 \times 1 + 3 \times 1 + 1 \times 1 = 5$. Constraints - For $20\%$ of the testdata: the input is guaranteed to be a tree, $1 \le n \le 8$, $v \le 5 \times 10^3$, and all $v$ are equal. - For $40\%$ of the testdata: $1 \le n \le 8$, $0 \le m \le 10^3$, $v \le 5 \times 10^3$, and all $v$ are equal. - For $70\%$ of the testdata: $1 \le n \le 8$, $0 \le m \le 10^3$, $v \le 5 \times 10^3$. - For $100\%$ of the testdata: $1 \le n \le 12$, $0 \le m \le 10^3$, $v \le 5 \times 10^5$. --- $\text{upd 2022.7.27}$: Added $50$ groups of hack testdata. Translated by ChatGPT 5