P3965 [TJOI2013] Cyclic Grid

A cyclic grid is a matrix in which every cell contains an arrow pointing to one of its four adjacent cells. Each cell has coordinates $(r, c)$, with the top-left cell at $(0, 0)$. Given a starting position $(r, c)$, you can move between cells following the arrows: if $(r, c)$ has a left arrow, move to $(r, c - 1)$; if it has a right arrow, move to $(r, c + 1)$; if it has an up arrow, move to $(r - 1, c)$; if it has a down arrow, move to $(r + 1, c)$. Each row and each column is cyclic: if you move out of bounds, you appear on the opposite side. For example, in a $5 \times 5$ cyclic grid, moving left from $(3, 0)$ will appear at $(3, 4)$.

A perfect cyclic grid is defined as follows: starting from any position, by following the arrows you will eventually return to the starting position. If a cyclic grid is not perfect, you may arbitrarily modify the arrow in any cell until it becomes perfect. For example, in the figure below, the grid on the left is not perfect, because only starting from $(1, 1)$, $(1, 2)$, $(2, 0)$, $(2, 3)$ will return to the starting position. By modifying two arrows, you obtain the grid on the right, which is perfect.  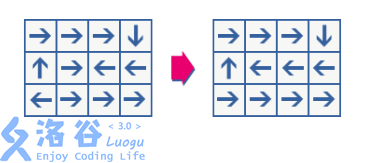Given a cyclic grid, compute the minimum number of cells you need to modify to make it perfect.

The first line contains two integers $R$ and $C$, the numbers of rows and columns of the cyclic grid. The next $R$ lines each contain $C$ characters, each being L, R, U, or D, indicating left, right, up, and down.

Output a single integer, the minimum number of cells that need to be modified to make the given cyclic grid perfect.

### Constraints 30% of the testdata: $1 \le R, C \le 7$. 100% of the testdata: $1 \le R, C \le 15$. Translated by ChatGPT 5