P3981 Langze's Puzzle

```cpp 万事万物总是那么巧妙，数学海洋令我无限徜徉，在那一瞬，我又发现了美。 ``` The great mathematician Langze of Zhencheng Ocean responded to the call of the Hall Master of Zhencheng Ocean and took part in making this problem. Based on his thinking and calculations, he created an interesting problem. Here is his message for you:

The inspiration for this problem comes from the following data:  This data follows the “description method” rule: on the $ n+1 $-th layer, describe the data of the $ n $-th layer from left to right. The rule is as follows: starting from the first datum, whenever you encounter a run of $ a_1 $ consecutive $ b_1 $, write $ a_1\,b_1 $ as two new data at the end of the $ n+1 $-th layer (the “end” here means appended after the last datum; if the $ n+1 $-th layer has no data yet, then this “end” is the beginning). Then, immediately describe the next run of $ a_2 $ consecutive $ b_2 $ ($ b_1 \neq b_2 $), and so on, until all data have been fully described. At that point, the $ n+1 $-th layer is constructed. Here $ n $ is a positive integer. Now, I have a new idea. Given an initial datum $ Q $ (the initial datum is on the first layer, and the first layer contains only one datum — the initial datum $ Q $), construct a data array using a rule similar to the one above (the description method), called the “Langze Array.” My rule is: on odd-numbered layers follow rule $ A $, and on even-numbered layers follow rule $ B $. See the figure below:  The above shows part of the Langze Array when the initial datum is $ 1 $. As for what the exact rules are, that is for you to explore. However!!! That is not the final goal. What I want you to find is: on the $ i $-th layer, how many $ x $ are there (we define the layer containing the initial datum as the first layer)?

The input contains only one line with three integers $ Q $, $ i $, and $ x $, separated by single spaces. $ Q $ is the initial datum of the Langze Array.

Output a single line with one integer: the count of $ x $ on the $ i $-th layer. Since the output can be large, output the result modulo $ 20171111 $ (that is, take the remainder after dividing the original result by $ 20171111 $).

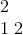
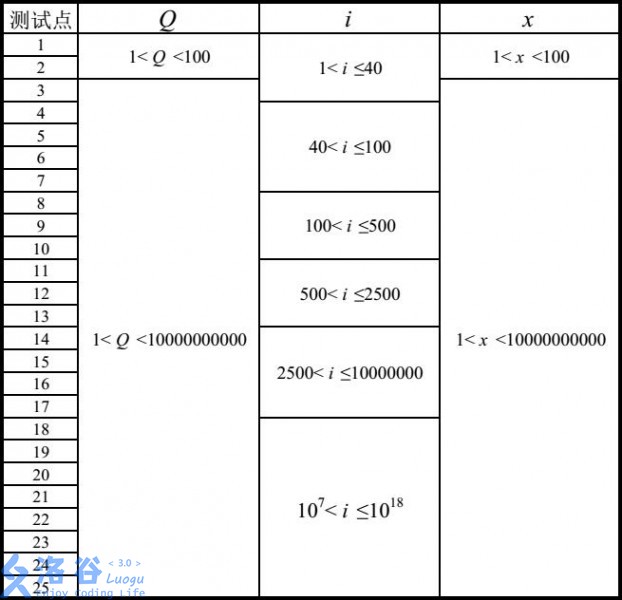
Sample 1 explanation: A (small) part of the constructed Langze Array is:  Therefore, the count of $ 2 $ on the $ 2 $-nd layer is $ 1 $. Notes: - All data are integers. - If you have no idea how to proceed, you may choose to solve some subproblems first. - Constraints for each test point are as follows:  Translated by ChatGPT 5