P3995 Heavy-Light Decomposition

Heavy-light decomposition is a computing term for an algorithm that partitions a tree. It first splits the tree into multiple chains via heavy-light edge decomposition, ensuring each node belongs to exactly one chain, and then maintains each chain using data structures (Fenwick tree, SBT, SPLAY, segment tree, etc.). (from Baidu Baike)

Daning has been studying heavy-light decomposition. He found that the time complexity of heavy-light decomposition mainly depends on how heavy and light chains are divided, and the most common method is to split according to subtree size. As shown in the figure (from Baidu Baike), black edges are heavy chains (arbitrary length), and white edges are light chains (all of length $1$. Note that in the figure, $1$–$2$ and $1$–$3$ are different light chains.  For each node, its child on the heavy chain is called its heavy child, and there is exactly one; leaf nodes have no heavy child. For example, for node $1$ in the figure, its heavy child is node $4$. Clearly, different decompositions lead to different numbers of chains visited by the same set of queries. Now, given a rooted tree with root $1$ and several queries, each query traverses all heavy-light chains along the path from $u$ to $v$ once. For example, under the decomposition in the figure above, the query from $3$ to $8$ visits $3$ chains in total: the light chain $1$–$3$, the heavy chain $1$–$4$, and the light chain $4$–$8$; the query from $3$ to $11$ also visits $3$ chains: the light chain $1$–$3$, the light chain $1$–$2$, and the heavy chain $2$–$11$. Please output a decomposition scheme that minimizes the total number of heavy-light chains visited over all queries. Since there may be many valid schemes, output any one of them. We provide a Special Judge to check the correctness of your scheme. Let the total number of chains visited by your scheme be $x$, by the standard solution be $x_0$, and let the scoring parameter be $a$. Your score is: - $10$ points if $x \leq x_0$. - $8$ points if $0 < (x - x_0) \leq a$. - $7$ points if $a < (x - x_0) \leq 2 \times a$. - $6$ points if $2 \times a < (x - x_0) \leq 3 \times a$. - $1$ point if you output a valid scheme. $a = \lfloor \frac{q}{300} \rfloor$, where $q$ is the number of queries. We provide `Div_Checker.exe` to check your answer. Put it in the same folder as `div.in` and `div.out`, then run it, where `div.in` is the input file and `div.out` is your program’s output on that input. 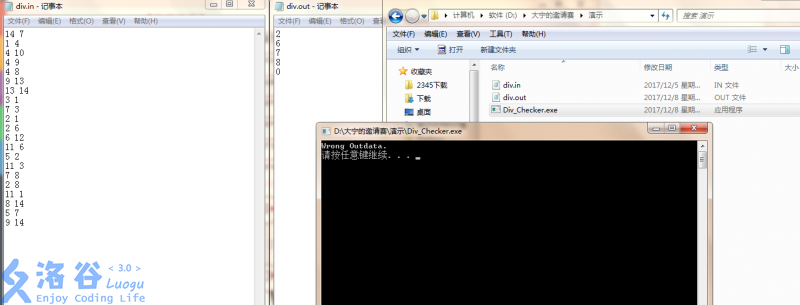If your `div.out` is valid, it will print: `Your answer is XXX.` `XXX` is the total number of chains visited by your decomposition on that input. Otherwise, it will print: `Wrong Outdata.` Note: You must not use file I/O in the official submission.

The first line contains two positive integers $n$ and $q$, the number of nodes of the tree and the number of queries. The next $n - 1$ lines each contain two positive integers $u$, $v$, meaning there is an edge between $u$ and $v$. The next $q$ lines each describe a query with two integers $U$, $V$, meaning a query from $U$ to $V$.

Output $n$ lines. For node $i$, if it is not a leaf, output its heavy child in your decomposition; otherwise, output $0$.

The sample corresponds to the figure above, but the decomposition in the figure is not optimal for the sample queries. Constraints: - For $20\%$ of the testdata, $n, q \leq 10$. - For $60\%$ of the testdata, $n, q \leq 1000$. - For $100\%$ of the testdata, $1 \leq n \leq 100000$, $1 \leq q \leq 200000$. It is guaranteed the input is a valid tree. [Div_Checker download](https://pan.baidu.com/s/1c26OLf6) If you are not sure how to use the checker, please refer to the images below. The data in the images is the sample.  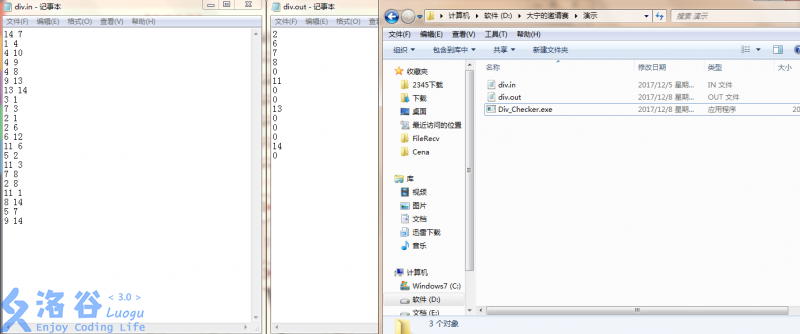An output of a valid scheme.  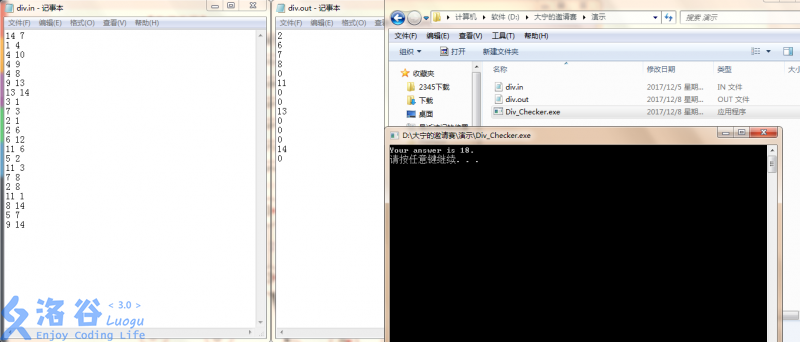An invalid output.  --- $\text{upd 2022.8.26}$: Added a new set of hack testdata. Translated by ChatGPT 5