P4007 [Tsinghua Training 2017] Xiao Y and the "Terrifying Slave Owner"

“A fight? Count me in!” Count me in for a fight. “Everyone, get in here!” Everyone, come here!

Xiao Y is an OIer who likes playing games. One day, she is playing a game and needs to fight a Boss. Although this Boss has $10^{100}$ HP, it only brings one minion — a "Terrifying Slave Owner" with exactly $m$ HP. This "Terrifying Slave Owner" has a special skill: whenever it takes damage but does not die (death means HP $ \leq 0$), and the number of the Boss's minions is less than the cap $k$, it summons a new "Terrifying Slave Owner" with $m$ HP. Now Xiao Y can make $n$ attacks. Each time she attacks, she chooses uniformly at random one target from the set consisting of the Boss and all of the Boss's minions, and reduces that target's HP by $1$. She wants to know the expected total HP deducted from the Boss after $n$ attacks. To avoid precision issues, your answer should be taken modulo $998244353$.

The first line contains three positive integers $T, m, k$, where $T$ is the number of queries, and $m, k$ are as defined in the statement. Then follow $T$ lines. Each line contains a positive integer $n$, representing a query asking for the expected HP deducted from the Boss after $n$ attacks.

Output $T$ lines. For each query, output a non-negative integer — the answer modulo $998244353$. It can be proven that the desired expectation is a rational number. Suppose it equals $p / q$ $(\mathrm{gcd}(p,q) = 1)$. Then the number $x$ you output should satisfy $p \equiv qx \pmod{998244353}$.

[Sample 1 Explanation] For the first query, the first attack has probability $\frac{1}{2}$ to hit the Boss and probability $\frac{1}{2}$ to hit the minion, so the answer is $\frac{1}{2}$. $1 \equiv 2 \times 499122177 \pmod{998244353}$. For the second query: if the first attack hits the Boss, then there is probability $\frac{1}{2}$ that the second attack still hits the Boss and probability $\frac{1}{2}$ that it hits the minion; if the first attack hits the minion, then a new minion (the "Terrifying Slave Owner") is summoned, so there is probability $\frac{1}{3}$ that the second attack hits the Boss and probability $\frac{2}{3}$ that it hits a minion. Therefore the answer is $\frac{1}{2}\times\frac{1}{2}\times2+\frac{1}{2}\times\frac{1}{2}\times1+\frac{1}{2}\times\frac{1}{3}\times1+\frac{1}{2}\times\frac{2}{3}\times0 = \frac{11}{12}$. $11 \equiv 12 \times 415935148\pmod{998244353}$. [Tips] The order of problems may not correspond to difficulty. 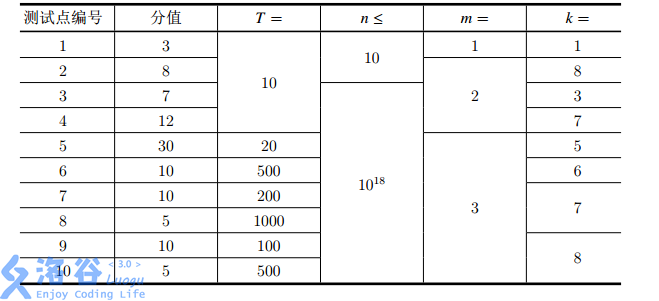[Subtasks] Across all test points, $1 \leq T \leq 1000, 1 \leq n \leq {10}^{18}, 1 \leq m \leq 3, 1 \leq k \leq 8$. The scores and Constraints for each test point are as follows:  Translated by ChatGPT 5