P4009 Car Refueling on a Grid

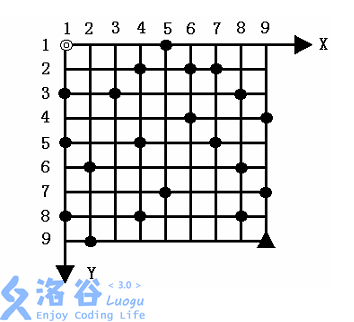
Given an $N \times N$ square grid with the top-left corner as the start point ◎ at coordinates $(1, 1)$, where the $X$-axis increases to the right and the $Y$-axis increases downward, and each grid cell has side length $1$, as shown in the figure.  A car starts from ◎ and drives to the bottom-right corner ▲ at coordinates $(N, N)$. Fuel depots are set at some grid intersections, where the car can refuel during the trip. The car must follow these rules: 1. The car can move only along grid edges, and with a full tank it can travel $K$ grid edges. The car starts with a full tank. There are no depots at the start or end points. 2. When the car traverses a grid edge, if its $X$-coordinate or $Y$-coordinate decreases, it must pay a fee of $B$; otherwise, there is no fee. 3. When the car encounters a depot during the trip, it must refuel to full and pay a refueling cost of $A$. 4. When needed, a new depot may be added at a grid point by paying an installation cost of $C$ (this does not include the refueling cost $A$). 5. $N, K, A, B, C$ are all positive integers and satisfy the constraints $2 \leq N \leq 100, 2 \leq K \leq 10$. Design an algorithm to compute the minimum total cost for the car to travel from the start to the destination.

The first line contains the values of $N, K, A, B, C$. Starting from the second line, an $N \times N$ binary matrix is given, ending at line $N + 1$, with $N$ values per row. If the value at row $i$, column $j$ is $1$, it means a fuel depot is set at the grid intersection $(i, j)$; if it is $0$, no depot is set there. Adjacent numbers in the same row are separated by spaces.

Output the minimum total cost at the end of the program.

Constraints: $2 \leq N \leq 100, 2 \leq K \leq 10$. Translated by ChatGPT 5