P4013 Number Trapezoid Problem

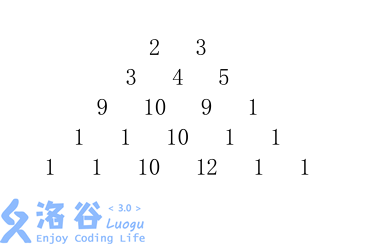
Given a number trapezoid with $n$ rows as shown in the figure.  The first row of the trapezoid contains $m$ numbers. Starting from each of the $m$ numbers in the top row, you may move at each step to the lower-left or lower-right adjacent number, forming a path from the top to the bottom of the trapezoid. Respect the following rules respectively: 1. The $m$ top-to-bottom paths are pairwise disjoint (no common nodes or edges). 2. The $m$ top-to-bottom paths may intersect only at numeric nodes (shared nodes allowed, shared edges not allowed). 3. The $m$ top-to-bottom paths may intersect at numeric nodes or along edges (both nodes and edges may be shared).

The first line contains two positive integers $m$ and $n$, denoting that the first row of the number trapezoid has $m$ numbers and there are $n$ rows in total. The next $n$ lines give the numbers in each row of the trapezoid. Row $1$ has $m$ numbers, row $2$ has $m+1$ numbers, and so on.

Output the maximum total sum computed under Rule $1$, Rule $2$, and Rule $3$, respectively, one maximum sum per line.

$1 \leq m,n \leq 20$. Translated by ChatGPT 5