P4020 [CTSC2012] 电阻网络

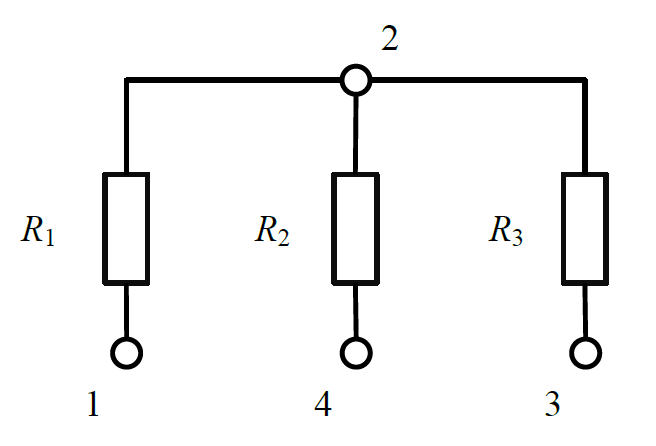
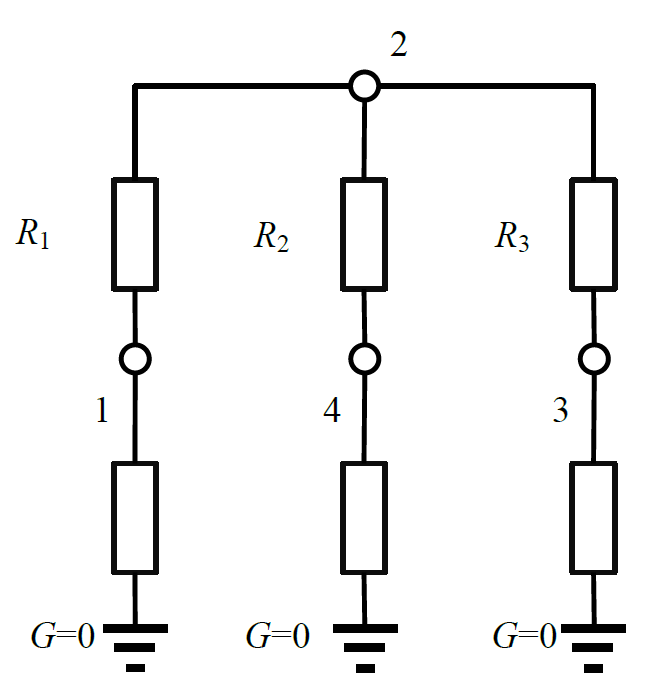
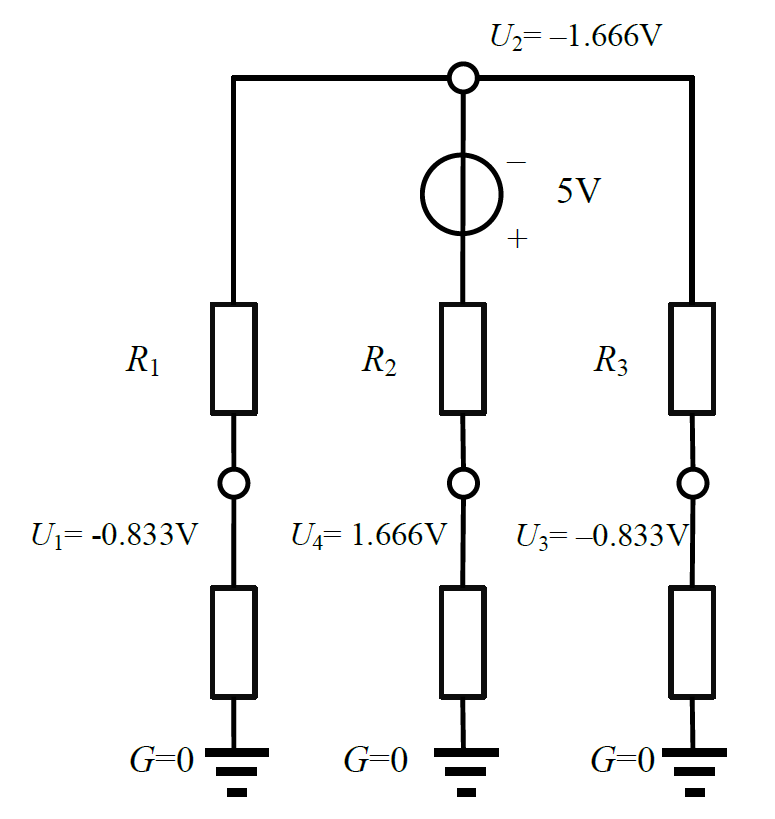
给定一个树型电网，树中的每条边上有一个电阻 $R_i$，电阻值均为 $10000\ Ω$。下图为一个包含 $4$ 个节点的树型电路情况：  树中的所有叶子节点（度为 $1$ 的节点称为叶子）都接地，每条线上都接地，每条线上都附有 $10000\ Ω$ 的电阻，最终形成的电网如下图所示：  现有如下两种操作： `C u v w`：表示在边 $(u,v)$ 上串联一个电源，电源的大小为 $w$ 伏，电源位于靠近节点 $u$ 一侧（如下图所示），电源负极指向 $u$。注意同一条边上可以串联多个电源。  `Q u` ：表示询问点 $u$ 当前的电压，此是指对地。 如对上图进行 `C 2 4 5` 操作后，网络变为：  此时每个节点上的电压见上图的标注。

输入文件 circuit.in 的第一行包含两个整数 $N,M$，分别表示树的节点数和操作个数。接下来 $N-1$ 行，每行两个数 $u,v$，表示有一条连接节点 $u,v$ 的边，这条边上恰好包含一个电阻。 接下来 $M$ 行，每行一个命令，格式见题目描述。

输出文件为 circuit.out。对于每个 `Q` 命令，输出一个数表示此刻该点的电压值。你可以输出任意多位的小数，只要你的答案和标准答案相差不超过 $10^{-3}$ 就算合法。

【样例说明】 对于第一个询问，由于原图中没有电源，所以没有电流，所有点的电压都相 等（否则如果有 $U_i>U_j$，则就有 $i$ 流向 $j$ 的电流，与没有电源矛盾），都等于地电压 $0\text{V}$。 之后在 $(2,4)$ 中加一个 $5\text{V}$ 的电源，得到的新图见题目描述。 整理后可以发现，新图的形式是串联（电源，$R_2+10000$，并联（$R_1+10000$，$R_3+10000$）），由此可以得到新图的总电阻为: $$ R 2 +10000+\frac{1}{\frac{1}{R_3 +10000}+\frac{1}{R_1 +10000}}=30000\ Ω $$ 所以流过节点 $4$ 的电流就是 $\frac{5}{30000}\ A$，所以 $U_4=\frac{5}{3}V$，$U_2=U_4+R_2\cdot I-5=-\frac{5}{3}V$，由 于 $U_1$ 和 $U_3$ 形式对称，由分压关系可知 $U_1 =U_3 =U_2\times\frac{10000}{10000+10000}=-\frac{5}{6}V$。 【数据规模】 $30\%$ 的数据保证 $N,M ≤ 30$。 $60\%$ 的数据保证 $N,M ≤ 3000$。 $100\%$ 的数据保证 $3 ≤ N,M ≤ 50000$，$1 ≤ u,v ≤ n$，$1 ≤ w ≤ 10$，树中最长链的长度不超过 $50$。