P4020 [CTSC2012] Resistor Network

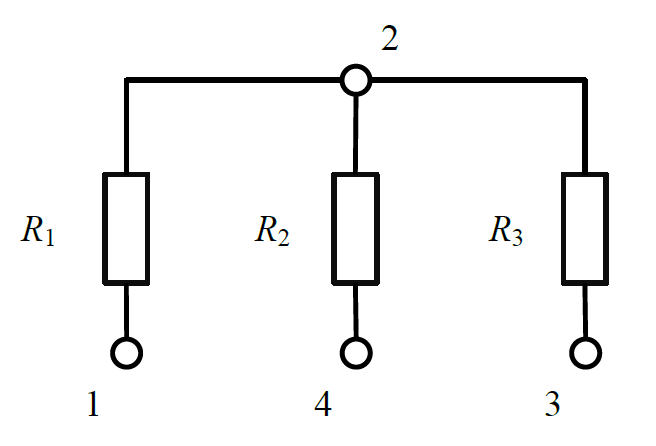
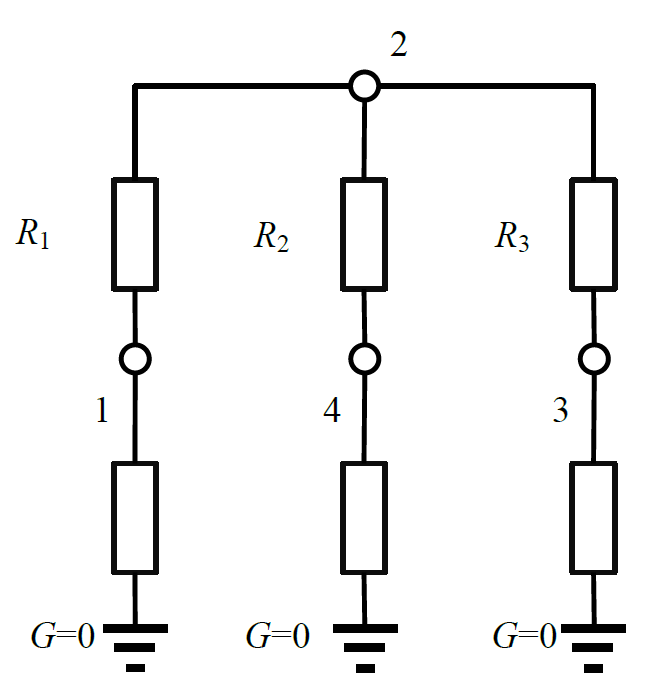
Given a tree-shaped circuit, each edge in the tree has a resistor $R_i$, and all resistances are $10000\ Ω$. The figure below shows a tree-shaped circuit with $4$ nodes:  All leaf nodes in the tree (nodes of degree $1$ are called leaves) are connected to ground, each line is connected to ground, and each line carries a $10000\ Ω$ resistor, forming the network shown below:  There are two types of operations: `C u v w`: Insert a voltage source in series on edge $(u, v)$, with magnitude $w$ volts. The source is placed on the side closer to node $u$ (as shown below), with its negative terminal pointing toward $u$. Note that multiple voltage sources can be inserted in series on the same edge.  `Q u`: Query the current voltage of node $u$, measured with respect to ground. 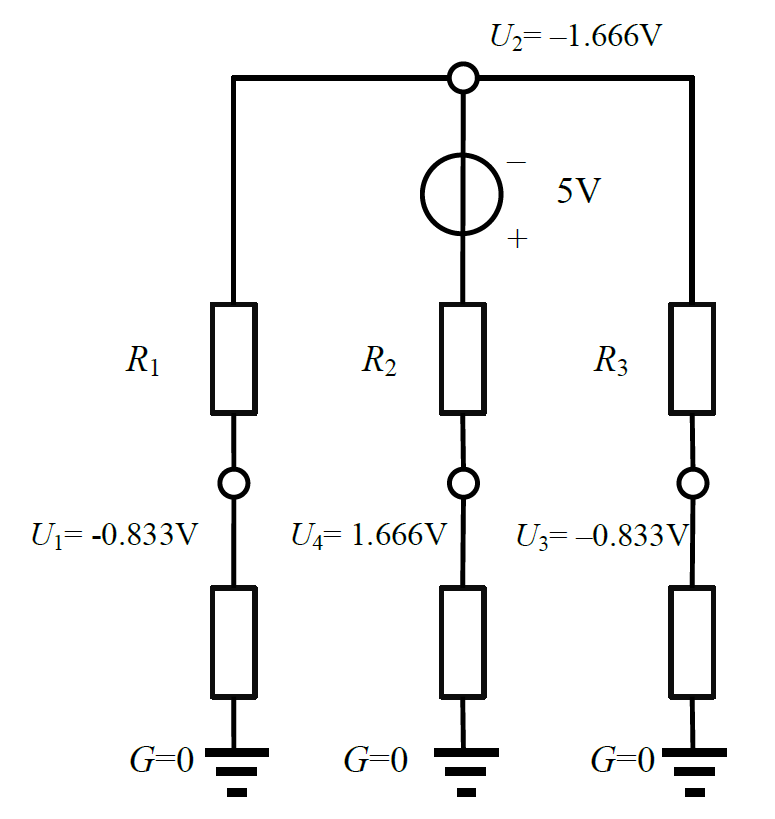After performing `C 2 4 5` on the figure above, the network becomes:  At this time, the voltage at each node is as labeled in the figure.

The input file circuit.in contains two integers $N, M$ on the first line, representing the number of nodes in the tree and the number of operations, respectively. The next $N-1$ lines each contain two integers $u, v$, indicating that there is an edge connecting nodes $u$ and $v$, and this edge contains exactly one resistor. Then there are $M$ lines, each containing one command in the format described above.

Output to circuit.out. For each `Q` command, output a single number representing the voltage at that node at that moment. You may print any number of decimal places; your answer is considered correct if it differs from the standard answer by at most $10^{-3}$.

[Sample Explanation] For the first query, since there is no voltage source in the original circuit, there is no current, and all node voltages are equal (otherwise, if there exists $U_i > U_j$, there would be current flowing from $i$ to $j$, contradicting the absence of a source). They are all equal to the ground potential $0\text{V}$. After adding a $5\text{V}$ voltage source on $(2, 4)$, the new circuit is as shown in the problem statement. After simplification, the new circuit can be seen as series (source, $R_2+10000$, parallel ($R_1+10000$, $R_3+10000$)), hence the equivalent resistance is: $$ R 2 +10000+\frac{1}{\frac{1}{R_3 +10000}+\frac{1}{R_1 +10000}}=30000\ Ω $$ Therefore, the current flowing through node $4$ is $\frac{5}{30000}\ A$, so $U_4=\frac{5}{3}V$ and $U_2=U_4+R_2\cdot I-5=-\frac{5}{3}V$; since $U_1$ and $U_3$ are symmetric, by the voltage division relation we have $U_1 =U_3 =U_2\times\frac{10000}{10000+10000}=-\frac{5}{6}V$. [Constraints] $30\%$ of the testdata guarantees $N, M ≤ 30$. $60\%$ of the testdata guarantees $N, M ≤ 3000$. $100\%$ of the testdata guarantees $3 ≤ N, M ≤ 50000$, $1 ≤ u, v ≤ n$, $1 ≤ w ≤ 10$, and the length of the longest chain in the tree does not exceed $50$. Translated by ChatGPT 5