P4080 [SDOI2016] Ordinary Die
Background
# Description
This is an ordinary die. It is a homogeneous convex polyhedron with $n$ vertices and $f$ faces. Each face is a convex polygon, and any two faces are not coplanar. When the die is thrown into the air, it will not bounce a second time upon landing (an idealized assumption).
You want to know the probability that each face ends up on the ground. The probability for each face can be computed as follows: let $O$ be the center of mass of the die, and let $S$ be the unit sphere of radius $1$ centered at $O$.
The surface area of $S$ is the surface area of the unit sphere, namely $4\pi$, where $\pi$ is the circle constant. For a face $C$ of the die, there exists a region $T$ on the sphere $S$ such that: when the die falls, if the direction of gravity intersects $S$ at a point within $T$, then $C$ is the face that ultimately lands on the ground. Therefore, the probability that $C$ lands is the area of region $T$ divided by $4\pi$.
To better assist in computing areas of regions on the sphere, we provide the area formula for a spherical triangle on the unit sphere $S$. Consider three pairwise intersecting great circles on $S$, with intersection points $A$, $B$, and $C$ in order. Then the area of the spherical triangle $ABC$ is $\text{Area}(ABC)=\alpha+\beta+\gamma-\pi$, where $\alpha,\beta , \gamma$ are the three angles. See the figure below.
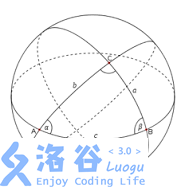
We guarantee that whenever a face lands on the ground, the orthogonal projection of the center of mass onto that face lies strictly inside the face. In other words, the die will not wobble unstably.
Description
This is an ordinary die. It is a homogeneous convex polyhedron with $n$ vertices and $f$ faces. Each face is a convex polygon, and any two faces are not coplanar. When the die is thrown into the air, it will not bounce a second time upon landing (an idealized assumption).
You want to know the probability that each face ends up on the ground. The probability for each face can be computed as follows: let $O$ be the center of mass of the die, and let $S$ be the unit sphere of radius $1$ centered at $O$.
The surface area of $S$ is the surface area of the unit sphere, namely $4\pi$, where $\pi$ is the circle constant. For a face $C$ of the die, there exists a region $T$ on the sphere $S$ such that: when the die falls, if the direction of gravity intersects $S$ at a point within $T$, then $C$ is the face that ultimately lands on the ground. Therefore, the probability that $C$ lands is the area of region $T$ divided by $4\pi$.
To better assist in computing areas of regions on the sphere, we provide the area formula for a spherical triangle on the unit sphere $S$. Consider three pairwise intersecting great circles on $S$, with intersection points $A$, $B$, and $C$ in order. Then the area of the spherical triangle $ABC$ is $\text{Area}(ABC)=\alpha+\beta+\gamma-\pi$, where $\alpha,\beta , \gamma$ are the three angles. See the figure below.

We guarantee that whenever a face lands on the ground, the orthogonal projection of the center of mass onto that face lies strictly inside the face. In other words, the die will not wobble unstably.
# Description
Input Format
The first line contains two integers, the total number of vertices $n$ and the total number of faces $f$. Vertex indices are $1$-indexed.
The next $n$ lines each contain three floating-point numbers $x$, $y$, and $z$, giving the coordinates of each vertex.
The next $f$ lines each describe one face. Each line begins with an integer $d \ge 3$ indicating the number of vertices on that face, followed by $d$ integers giving, in counterclockwise order as seen from outside the die, the indices of the vertices.
Output Format
Output $f$ lines. The $i$-th line contains a floating-point number, which is the probability that the $i$-th face lands on the ground. Your output should keep 7 digits after the decimal and be the value closest to the reference answer under the constraint of keeping 7 decimal places. The testdata guarantees that there is no precision ambiguity caused by rounding at the 8th decimal place.
Explanation/Hint
Constraints:
- For all testdata, $4 \le n \le 50$ and $4 \le f \le 50$.
- The absolute value of each coordinate is at most $10000$.
Translated by ChatGPT 5