P4096 [HEOI2013] Eden's Game Tree

# Description For a two-player, perfect-information, deterministic game, a game tree is a common analysis tool. A game tree is a rooted tree whose nodes are game states. If node B’s parent is A, then state A can transition to state B with a single decision. Each state has a unique player to move, i.e., exactly one side should make the move at that state. We assume the two players alternate moves at all times, meaning adjacent nodes in the tree always have different players to move. In this problem, we only care about which player wins, and we assume the game cannot end in a draw. We call the two players Black and White, and the root’s player to move is Black. Clearly, each node has exactly two possible outcomes: Black wins or White wins. If an internal node (i.e., a node that has children) is a Black-to-move node, then this node is winning for Black if and only if at least one of its children is winning for Black; conversely for a White-to-move node. Solving the game tree means determining the outcome at the root. If we already knew the outcomes of all leaves (nodes without children), the game tree would be easy to solve. However, here the outcomes of all leaves are unknown and need further computation. For a set of leaves $S$, if knowing that every node in $S$ is a win for Black is sufficient to assert that the root is a win for Black, then $S$ is called a Black-winning set. Among Black-winning sets $S$, if for any other Black-winning set $S'$ it holds that $|S| \le |S'|$ (where $|S|$ denotes the number of elements in $S$), then $S$ is a minimal Black-winning set. Similarly, we can define White-winning sets and minimal White-winning sets. Eden is studying game trees. He noticed that if a leaf belongs to some minimal Black-winning set and also to some minimal White-winning set, then determining this leaf’s outcome is clearly most helpful for determining the root’s outcome. Such leaves are called critical leaf nodes. For a given game tree, Eden wants to know which leaves are critical leaf nodes.

对于有两个玩家的，状态透明且状态转移确定的博弈游戏，博弈树是常用的分析工具。博弈树是一棵有根树，其中的节点为游戏的状态。若节点 B 的父亲是 A，则说明状态 A 能通过一次决策转移到状态 B。每个状态都有一个唯一的决策方，即这个状态下应该由哪一方做出决策。我们规定双方在任何时候都是轮流做出决策的，即树上相邻节点的决策方总是不相同的。 在这个问题中，我们只关心两个玩家的胜负情况，且规定游戏不会出现平局。 我们称两个玩家分别为黑方和白方，其中根节点的决策方为黑方。显然每个节点只有两个状态：黑方胜和白方胜。若某内节点（即存在后继节点的节点）的决策方为黑方，则该节点为黑方胜的充要条件为它的儿子中存在黑方胜的节点，反之亦然。求解博弈树即为判明博弈树根节点的状态。 如果我们得知了所有叶节点（即无后继节点的节点）的状态，那么博弈树就很容易求解了。但是现在的情况是所有叶节点的状态均为未知的，需要进一步的计算。对于一个由叶节点构成的集合 $S$，如果 $S$ 中的节点均被判明为黑方胜，就可以断言根节点为黑方胜的话，则称 $S$ 为一个黑方胜集合。对于黑方胜集合 $S$， 如果对于任意的黑方胜集合 $S'$ 均满足 $|S| \le |S'|$（$|S|$ 表示集合 $S$ 中的元素数目）， 则称 $S$ 为一个最小黑方胜集合。同样地，也可以定义白方胜集合和最小白方胜集合。 Eden 最近在研究博弈树问题。他发现，如果一个叶节点既属于某一个最小黑方胜集合，又属于一个最小白方胜集合，那么求解这个节点的状态显然最有益于求解根节点的状态。像这样的叶节点就称之为关键叶节点。对于一棵给定的博弈树，Eden 想要知道哪些叶节点是关键叶节点。

每个测试点包含一组测试数据。 测试数据的第一行包含一个正整数 $n$，表示博弈树的节点数目。节点从 $1$ 到 $n$ 编号，且 $1$ 号节点为根节点。 之后 $n - 1$ 行，每行包含一个正整数。第 $i$ 行的正整数表示节点 $i$ 的父节点的编号。

Print three space-separated positive integers on a single line: the index of the critical leaf node with the smallest index, the number of critical leaf nodes, and the bitwise XOR of the indices of all critical leaf nodes.

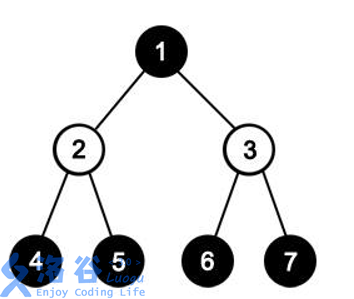
[Sample explanation]  As shown, black nodes indicate Black-to-move nodes, and white nodes indicate White-to-move nodes. All minimal Black-winning sets are $\{4, 5\}$ and $\{6, 7\}$. All minimal White-winning sets are $\{4, 6\}$, $\{4, 7\}$, $\{5, 6\}$, and $\{5, 7\}$. Therefore, the set of critical leaf nodes is $\{4, 5, 6, 7\}$. - For $30\%$ of the testdata, $n \le 100$. - For $40\%$ of the testdata, $n \le 1000$. - For $50\%$ of the testdata, $n \le 10 ^ 4$, and the tree is randomly generated. - For $100\%$ of the testdata, $1 \le n \le 2\times 10 ^ 5$, and for node $i$ ($i \ne 1$), the index of its parent is less than $i$. Translated by ChatGPT 5