P4120 [WC2012] 最小生成树

给定无向带权连通图$G$，我们希望通过修改边的权值，使它的最小生成树唯一，已知减小，增加一条边的权值的单位代价分别为 $a$ 和 $b$，且修改后的权值必须为非负整数。 例如，对某个图 $G$，如果将一条边的权值减 $3$，另一条边的权值加 $2$ 之后，它的最小生成树唯一，则此时的代价之和是 $3a+2b$。试计算代价之和的最小值。

从文件mst.in中读入数据。 第一行包含字符串“$mst$” 和数据编号。 第二行包含 $4$ 个正整数 $n$,$m$,$a$,$b$，分别表示图 $G$ 顶点的个数，边的条数，以及对一条边的权值减小 $1$，增加 $1$ 的代价。 接下来 $m$ 行，每行 $3$ 个正整数 $x$,$y$,$w$，表示顶点 $x$ 和顶点 $y$ 之间有一条初始权值为 $w$ 的边。 顶点由 $1$ 至 $n$ 编号。

输出到文件mst.out中。 输出文件仅一行，包含一个整数，表示最小代价，无需修改则输出 $0$。

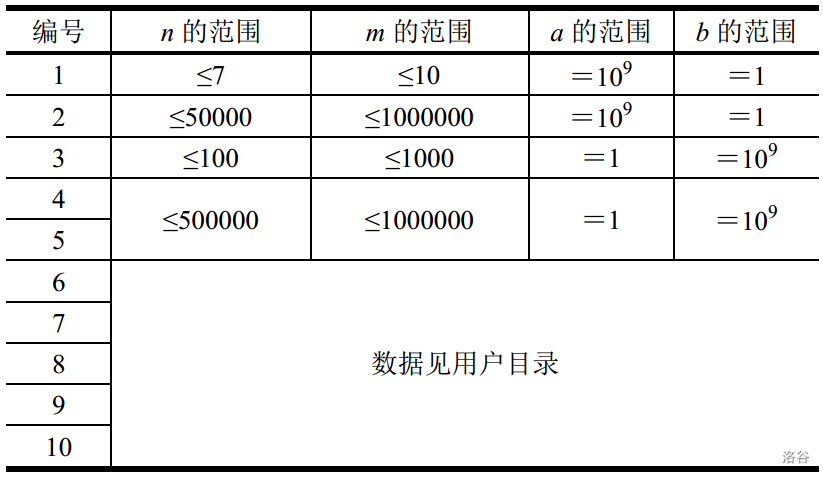
【样例说明】 将边$(2,4)$的权值减 $1$，边$(2,3)$的权值加 $1$ 之后，图 $G$ 的最小生成树唯一，且此时的代价之和为最小值。 【数据范围】  [测试点$6$~$10$下载](https://pan.baidu.com/s/1bqiS6w3)