P4120 [WC2012] Minimum Spanning Tree

Given an undirected, weighted, connected graph $G$, we want to modify edge weights so that its minimum spanning tree is unique. The unit costs to decrease and increase the weight of an edge by 1 are $a$ and $b$, respectively, and the modified weights must be non-negative integers. For example, for some graph $G$, if after decreasing the weight of one edge by $3$ and increasing the weight of another edge by $2$ the minimum spanning tree becomes unique, then the total cost is $3a+2b$. Compute the minimal total cost.

Read from standard input. The first line contains the string “$mst$” and a testdata ID. The second line contains 4 positive integers $n$, $m$, $a$, $b$, denoting the number of vertices of $G$, the number of edges, and the unit costs to decrease an edge weight by $1$ and to increase it by $1$, respectively. Each of the next $m$ lines contains 3 positive integers $x$, $y$, $w$, indicating that there is an edge between vertices $x$ and $y$ with initial weight $w$. Vertices are numbered from $1$ to $n$.

Write to standard output. Output a single line containing one integer, the minimal total cost. If no modification is needed, output $0$.

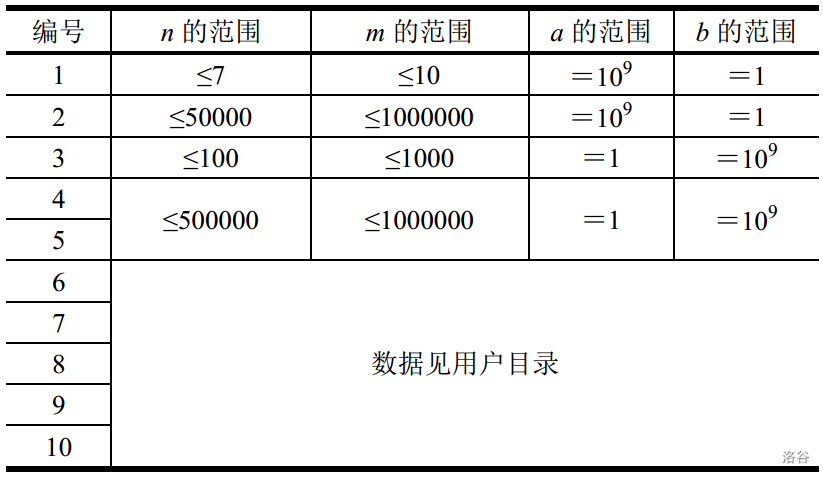
[Sample explanation] After decreasing the weight of edge $(2,4)$ by $1$ and increasing the weight of edge $(2,3)$ by $1$, the minimum spanning tree of graph $G$ becomes unique, and the total cost is minimal. [Constraints]  [Test points $6$~$10$ download](https://pan.baidu.com/s/1bqiS6w3) Translated by ChatGPT 5