P4129 [NEERC 2005 / SHOI2006] Cactus

This problem is different from bzoj1023. Luogu quick access to bzoj1023: [[SHOI2008] Cactus II](/problem/P4244).

A cactus is an undirected connected graph in which each edge appears in at most one simple cycle. Intuitively, a cactus can be viewed as a tree that is allowed to have cycles. There is, however, a fundamental difference between cacti and trees: a cactus can have multiple connected spanning subgraphs, whereas a tree has only one (itself). We call the number of connected spanning subgraphs the “Xian” number (xiān). Your task is to compute the “Xian” number of the given graph. 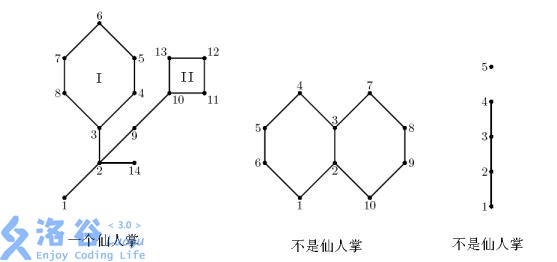Some examples of cacti:  The first figure is a cactus. In the second figure, the edge $(2,3)$ lies on two different cycles, so it is not a cactus. The third figure is not connected, so it is not a cactus either. Explanations of some terms: - Simple cycle: A simple cycle is a path in the original graph whose edge set forms a cycle, and each vertex appears at most once in the cycle. For example, for the second figure above, it has three simple cycles: $(4,3,2,1,6,5)$, $(7,8,9,10,2,3)$, and $(4,3,7,8,9,10,2,1,6,5)$. - Spanning subgraph: A spanning subgraph is also a subgraph of the original graph; it may have fewer edges, but it must preserve connectivity and must not remove any vertices of the original graph. The notion of “spanning” is similar to that in the familiar “minimum spanning tree.” For the first figure above, removing any one edge in cycle I or any one edge in cycle II yields a spanning subgraph, so the total number of spanning subgraphs is $6 + 4 + 6 \times 4 + 1 = 35$ (note that a graph is also a subgraph of itself).

The first line contains two integers $n$ and $m$. The $n$ vertices are numbered from $1$ to $n$. Each of the next $m$ lines describes a path in the graph (note: such a path is not necessarily a cycle). The format of a line is: an integer $k_i$ indicating how many vertices this path goes through, followed by $k_i$ integers between $1$ and $n$, each denoting a vertex of the graph; consecutive vertices define an edge. A path may pass through the same vertex multiple times. For example, in the first figure, the first path goes from $2$ through $3$, and then returns to $3$ from $8$. We guarantee that every edge appears in exactly one path: no edge appears in two different paths, and no edge appears twice within a single path.

Output the graph’s “Xian” number. If it is not a cactus, output `0`. Note that the final answer can be very large.

For all testdata, $1 \le n \le 20000$, $0 \le m \le 1000$, and $2 \le k_i \le 1000$. Translated by ChatGPT 5