P4142 {{Cave Emergency}}

{{When ZRQ was about to collect minerals in the cave, an accident happened. The cave is about to collapse! Problem source: [zhoutb2333](https://www.luogu.org/space/show?uid=31564).}}

{{The entire cave is an $N*N$ grid. Each cell is denoted as $(X, Y)$, where $1 \le X, Y \le N$. Here $X$ is the row index from top to bottom, and $Y$ is the column index from left to right. $(1,1)$ is the top-left corner, $(1,N)$ is the top-right corner, $(N,1)$ is the bottom-left corner, and $(N,N)$ is the bottom-right corner. Cells with $X+Y$ odd have an instability $V_{X,Y}$, while cells with $X+Y$ even have instability $0$. ZRQ happens to have $M$ pillars that can support the cave. The strength of each pillar can be regarded as infinite. As long as a cell is supported, its instability becomes $0$. Each pillar is L-shaped: in addition to occupying its current cell (the corner), it must also occupy two adjacent cells so that the three cells form an L shape. You can place it in any of the $4$ orientations.  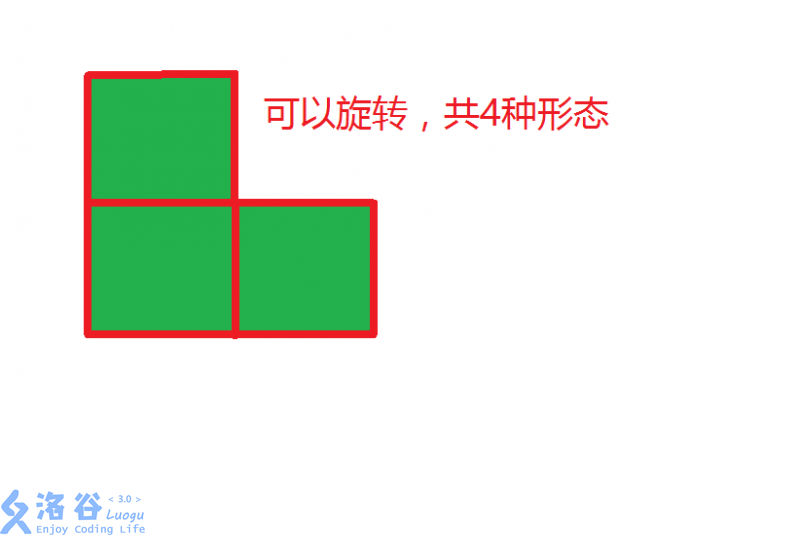Occupying adjacent cells with a pillar does not reduce their instability (in other words, a pillar only has force at its corner cell). Some cells have already collapsed, so you cannot place a pillar there, and these cells cannot be occupied either. There are $K$ such cells. Their instability is $0$ (even if $X+Y$ is odd, a collapsed cell’s instability is still $0$). ZRQ asks: after placing some pillars (you do not have to use all $M$ pillars), what is the minimum possible sum of instabilities?}}

{{The first line contains three integers $N, M, K$. The next $N$ lines each contain $N$ integers, representing the instability of each cell. It is guaranteed that cells with $X+Y$ even and collapsed cells have instability $0$. The next $K$ lines each contain two integers $X, Y$, denoting the coordinates of the collapsed cells.}}

{{Output a single integer: the minimum possible sum of instabilities.}}

{{There are $10$ test points, each worth $10$ points, for a total of $100$ points. Constraints: - For test points $1$–$3$: $1 \le N \le 6$. - For test points $4$–$7$: $1 \le N \le 11$. - For test points $8$–$10$: $1 \le N \le 50$. - For all test points: $0 \le M \le \frac{N^2}{3}$, $0 \le K \le N^2$, $0 \le V_{X,Y} \le 10^6$. Sample #1 explanation: It is clearly impossible to have any two unstable cells both covered by a pillar’s corner. Therefore, just cover $(2,1)$ with a pillar’s corner. The remaining instability is $V_{1,2}+V_{2,3}+V_{3,2}=1+1+1=3$. Sample #2 explanation: None can be placed. The remaining instability is $V_{1,2}+V_{2,3}+V_{3,2}=2+4+3=9$.}} Translated by ChatGPT 5