P4152 [WC2014] Spacetime Shuttle

Xiao X is piloting his spaceship to traverse an $n$-dimensional space, where each point is represented by $n$ real numbers, i.e., $(x_1, x_2, \dots, x_n)$. To pass through this space, Xiao X needs to choose $c$ ($c \geq 2$) points in this space as stopping places for the spaceship, and these points must satisfy the following three conditions: 1. Every coordinate of each point is a positive integer, and the $i$-th coordinate does not exceed $m_i$. 2. For $1 \leq i < c$ and $1 \leq j \leq n$, the $j$-th coordinate of the $(i+1)$-th point must be strictly greater than the $j$-th coordinate of the $i$-th point. 3. There exists a straight line passing through all the chosen points. In this $n$-dimensional space, a straight line can be represented by $2n$ real numbers $p_1$, $p_2$, … , $p_n$, $v_1$, $v_2$, … , $v_n$. A line passes through a point $(x_1, x_2, \dots, x_n)$ if and only if there exists a real number $t$ such that for $i = 1 \dots n$ it holds that $x_i$ = $p_i + tv_i$. Xiao X has not finalized his plan yet. Please help him compute how many different schemes satisfy his requirements. Since the answer may be very large, you only need to output the value of the answer mod $10 007$.

The first line contains a positive integer $T$, the number of test cases. For each test case, there are two lines: - The first line contains two positive integers $n$, $c$ ($c \geq 2$), denoting the dimension of the space and the number of stopping points to select. - The second line contains $n$ positive integers, which are $m_1$, $m_2$, … , $m_n$.

Output $T$ lines. Each line contains a non-negative integer, which is the answer for the corresponding test case.

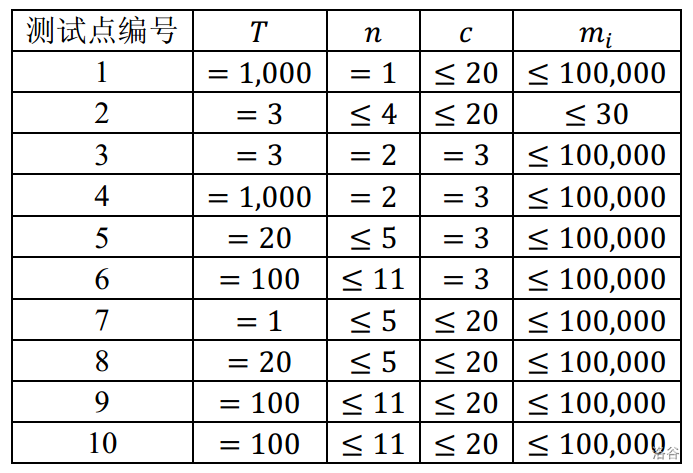
[Sample 1 Explanation] There are two feasible schemes in the first sample: one is to choose $(1,1)$, $(2,2)$, $(3,3)$; the other is to choose $(1,2)$, $(2,3)$, $(3,4)$. Constraints  Translated by ChatGPT 5