P4199 All Paths Deserted

Mr. Bao is a good driver who always drove students up the mountain for fun. But after his last trip last year, for some strange reasons, he changed careers. For half a year, no one has gone up the mountain along this road. When VFleaKing came back to this mountain, he found that the usual crowds of tourists were gone. Well, even when Mr. Bao was still around, not everyone coming to the mountain was there to enjoy the scenery.

If the computer room is about to close, or you are in a hurry, please skip directly to the sixth paragraph. VFleaKing noticed that along the dirt road going up and down the mountain, some places offer beautiful views while others do not. Divide the uphill road into segments of $10$ cm each. For every segment, use `a` to indicate that a nice view can be enjoyed, and `b` to indicate that it cannot. Then you get a string $s$ containing only `a` and `b`. Since going downhill uses the same road, the string for the downhill road is the reverse of the uphill string. Let the uphill string have length $n$, with characters $s_1, s_2, \ldots, s_n$ in order. On the way up and down, VFleaKing will choose certain segments to look at the scenery, and keep his head down the rest of the time. That is, VFleaKing chooses $k$ segments $x_1, x_2, \ldots, x_k$, where $k > 0$ and $1 \le x_1 < x_2 < \cdots < x_k \le n$, and he will look at the scenery at these positions both uphill and downhill.  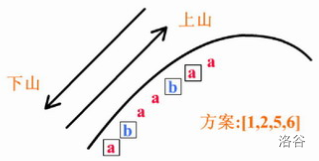VFleaKing wants the results of seeing scenery to be the same uphill and downhill. That is, the sequence of whether he sees scenery uphill is $s_{x_1}, s_{x_2}, \cdots, s_{x_k}$, denoted by $T_1$, and the sequence downhill is $s_{x_k}, s_{x_{k-1}}, \cdots, s_{x_1}$, denoted by $T_2$. VFleaKing wants $T_1 = T_2$. VFleaKing also wants the intervals between these checks to be equal uphill and downhill. That is, the uphill intervals are $x_2 - x_1, x_3 - x_2, \ldots, x_k - x_{k-1}$, denoted by $P_1$. The downhill intervals are $x_k - x_{k-1}, x_{k-1} - x_{k-2}, \ldots, x_2 - x_1$, denoted by $P_2$. VFleaKing wants $P_1 = P_2$. VFleaKing thinks that if, between the first and the last time he looks at the scenery, there is not a single moment when he keeps his head down, he will fall. That is, if for all $1 \le i \le k$ we have $x_i = x_1 + i - 1$, then VFleaKing will fall, and he does not want this to happen. In short, select a subsequence from a string containing only `a` and `b` such that: 1. Both positions and characters are symmetric about some axis. 2. It is not a contiguous segment. 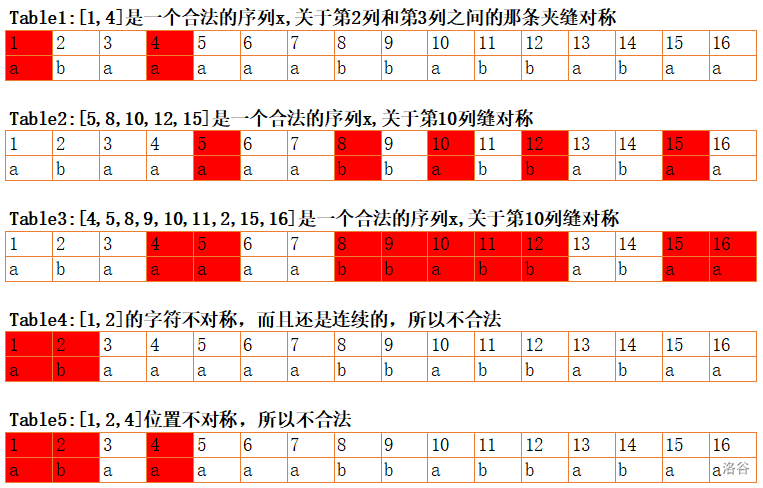Take $s = \texttt{"abaaaaabbabbabaa"}$ as an example. If we use $[a_1, a_2, \ldots, a_k]$ to denote a sequence, then $[1, 4]$ is a valid sequence $x$, $[5, 8, 10, 12, 15]$ is also valid, and $[4, 5, 8, 9, 10, 11, 12, 15, 16]$ is also valid. However, $[1, 2]$ does not satisfy VFleaKing’s first and third wishes, so it is not valid. $[1, 2, 4]$ does not satisfy the second wish, so it is not valid. $[9, 10, 11]$ does not satisfy the third wish, so it is not valid.  Given the string $s$, VFleaKing wants to know how many valid sequences $x$ there are. The answer can be large; please output it modulo $1000000007$.

One line, a string containing only the two characters `a` and `b`.

One line, a non-negative integer representing the answer.

Sample Explanation 1 There are $14$ valid sequences: - $[1, 3]$, $[1, 4]$, $[2, 5]$, $[1, 6]$, $[3, 6]$, $[4, 6]$, $[1, 7]$, $[3, 7]$, $[4, 7]$; - $[1, 4, 7]$, $[3, 5, 7]$; - $[1, 3, 4, 6]$, $[1, 2, 5, 6]$, $[3, 4, 6, 7]$. Sample Explanation 2 I have come up with a brilliant explanation, but there are too many cases to fit here. Sample Explanation 3 I have come up with a brilliant explanation, but there are too many cases to fit here. Constraints - For $10\%$ of the testdata, the string contains only the letter `a` or only the letter `b`. - For another $20\%$ of the testdata, $n \le 1000$. - For another $20\%$ of the testdata, either the number of `a` does not exceed $10$, or the number of `b` does not exceed $10$. - For another $10\%$ of the testdata, $n \le 10000$. - For $100\%$ of the testdata, $n \le 100000$. Source - 2013 Hubei Mutual Test week 1 - bzoj 3160 - A Mathematical Textbook for the Informatics Olympiad - Compiled by stong9070 Translated by ChatGPT 5