[NOI2005] 月下柠檬树

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。 李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？ 李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。 李哲将整棵柠檬树分成了 $n$ 层，由下向上依次将层编号为 $1,2,...,n$。从第 $1$ 到 $n-1$ 层，每层都是一个圆台型，第 $n$ 层(最上面一层)是圆锥型。对于圆台型， 其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第 $n$ 层(最上面一层)圆锥的底面就是第 $n-1$ 层圆台的上底面。所有的底面 的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为 $h_1,h_2,...,h_n$，第 $1$ 层圆台的下底面距地面的高度为 $h_0$，以及每层的下底面的圆的半径 $r_1,r_2,...,r_n$。李哲用熟知的方法测出了月亮的光线与地面的夹角为 $\mathrm{alpha}$。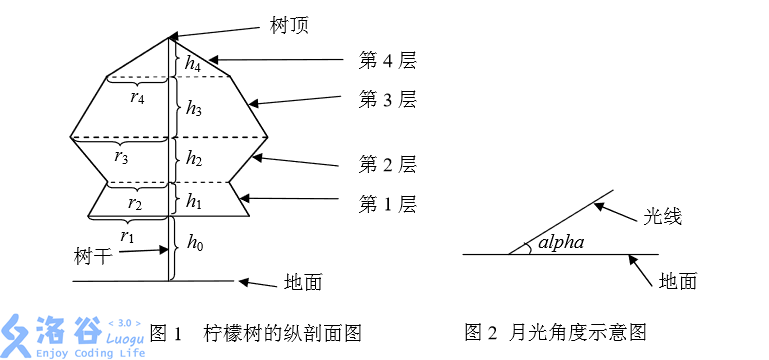  为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。李哲当然会算了，但是他希望你也来练练手。

第一行包含一个整数 $n$ 和一个实数 $\mathrm{alpha}$，表示柠檬树的层数和月亮 的光线与地面夹角（单位为弧度）。 第二行包含 $n+1$ 个实数 $h_0,h_1,h_2,...,h_n$ 表示树离地的高度和每层的高度。 第三行包含 $n$ 个实数 $r_1,r_2,...,r_n$ 表示柠檬树每层下底面的圆的半径。 同一行相邻的两个数之间用一个空格分隔。 输入的所有实数的小数点后可能包含一至十位有效数字。

输出一个实数，表示树影的面积，四舍五入保留两位小数。

2  0.7853981633 
10.0  10.00  10.00 
4.00  5.00

171.97

对于 $10 \%$ 的数据，$n \leq 1$； 对于 $30 \%$ 的数据，$n \leq 2$； 对于 $60 \%$ 的数据，$n \leq 20$； 对于 $100 \%$ 的数据，$1 \leq n \leq 500$，$0.3 < \mathrm{alpha} < \frac{\pi}{2}$，$0 < h_i \leq 100$，$0 < r_i \leq 100$。