P4227 [Tsinghua Training 2017] My Life Is Like a Candle in the Wind

Jiutiao Kelian is a playful girl. One day she nails $n$ nails into a wall. The $i$-th nail is at $(x_i, y_i)$. Then she nails $m$ ropes onto the wall. One endpoint of the $i$-th rope is the point $s_i (sx_i, sy_i)$, the rope passes through the point $t_i (tx_i, ty_i)$, and the rope length is $L_i$. The point $s_i$ is stuck to the wall, while the other endpoint is movable. Initially, the rope is a taut straight-line segment. Next, for each rope, Kelian plays a game once. In the $i$-th game, Kelian pinches the moving endpoint of the $i$-th rope and moves it clockwise, keeping the rope taut at every moment. It is not hard to see that, at every moment, the rope performs a clockwise circular motion around some center. 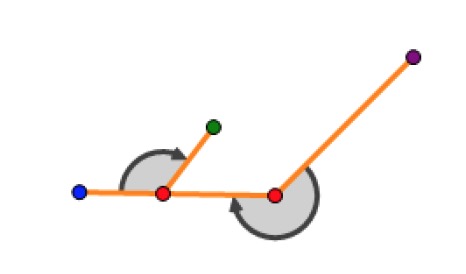Initially the center is the fixed endpoint $s$, but during the motion the center may keep changing, as shown below:  In the figure, the red dot on the left is a nail, the red dot on the right is the rope’s fixed endpoint, the other colored dots are virtual points, and the moving endpoint is the purple dot. The rope starts from the purple dot; when it reaches the blue dot, the rope wraps around the left red nail, so the moving endpoint switches its center and radius and continues a clockwise circular motion. Then the moving endpoint reaches the green dot, and thereafter it keeps circling around the left nail indefinitely. It is easy to see the rope’s motion never stops, so Kelian stops whenever she feels tired. However, being very curious, she decides to compute, for each rope, if it runs indefinitely, how many times its center will switch (including the initial center). This number is guaranteed to be finite. To simplify the problem, we make the following assumptions about the game: 1. During the motion, the Euclidean distance from the moving endpoint to every nail is always greater than or equal to $9 \times 10^{-4}$. 2. Nail coordinates are pairwise distinct, but there may be multiple collinear points. 3. The volumes of the nails and the rope are negligible. During the game, different segments of the rope do not interfere with each other. 4. Initially, the minimum Euclidean distance from the rope to every nail is greater than or equal to $9 \times 10^{-4}$. 5. The initially attached endpoint does not affect the rope’s motion, i.e., the rope will not wrap back onto its fixed endpoint.

Read from standard input. The first line contains an integer $T$, the number of test cases. For each test case, the first line contains two integers $n, m$, the number of nails and the number of ropes. The next $n$ lines each contain two integers $x_i, y_i$ giving the coordinates of the nails. The next $m$ lines each contain five integers $sx_i, sy_i, tx_i, ty_i, L_i$ describing a rope, as stated above.

Output to standard output. For each rope in each test case, output a single line with one integer: the number of times the center changes during the motion. Do not print extra blank lines between test cases.

For the first $10\%$ of the testdata, $n \leq 2$. For the first $20\%$ of the testdata, $n \leq 3$. For the first $30\%$ of the testdata, $n \leq 10$. For the first $60\%$ of the testdata, $n \leq 100, m \leq 100$. For $100\%$ of the testdata, $1 \leq n \leq 500$, $1 \leq m \leq 500$, $1 \leq T \leq 10$. For $100\%$ of the testdata, $0 \leq |x_i|, |y_i|, |sx_i|, |sy_i|, |tx_i|, |ty_i| \leq 10^4$. Translated by ChatGPT 5