P4295 [SCOI2003] 严格N元树
题目描述
如果一棵树的所有非叶节点都恰好有 $n$ 个儿子,那么我们称它为严格 $n$ 元树。如果该树中最底层的节点深度为 $d$(根的深度为 $0$),那么我们称它为一棵深度为 $d$ 的严格 $n$ 元树。例如,深度为2的严格2元树有三个,如下图:
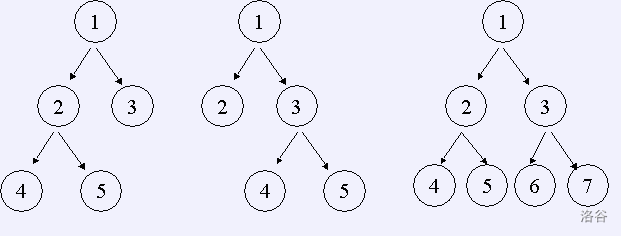
给出 $n,d$,编程数出深度为 $d$ 的 $n$ 元树数目。
输入格式
仅包含两个整数 $n,d(0
输出格式
仅包含一个数,即深度为 $d$ 的 $n$ 元树的数目。