P4295 [SCOI2003] Strict N-ary Tree

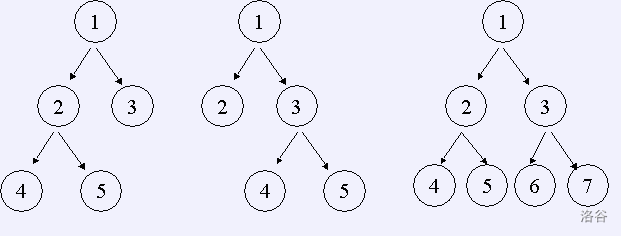
If every non-leaf node of a tree has exactly $n$ children, we call it a strict $n$-ary tree. If the deepest nodes in the tree have depth $d$ (the root has depth $0$), then we call it a strict $n$-ary tree of depth $d$. For example, there are three strict $2$-ary trees of depth $2$, as shown below:  Given $n, d$, write a program to count the number of strict $n$-ary trees of depth $d$.

Contains only two integers $n, d$ ($0 < n \le 32$, $0 \le d \le 16$). The testdata guarantees that you do not need to consider trees with more than $1024$ nodes on any level (i.e., $n^d \le 1024$).

Contains only one number, which is the number of strict $n$-ary trees of depth $d$.

The answer is guaranteed to be at most $200$ decimal digits. Translated by ChatGPT 5