P4306 [JSOI2010] Reachability Count

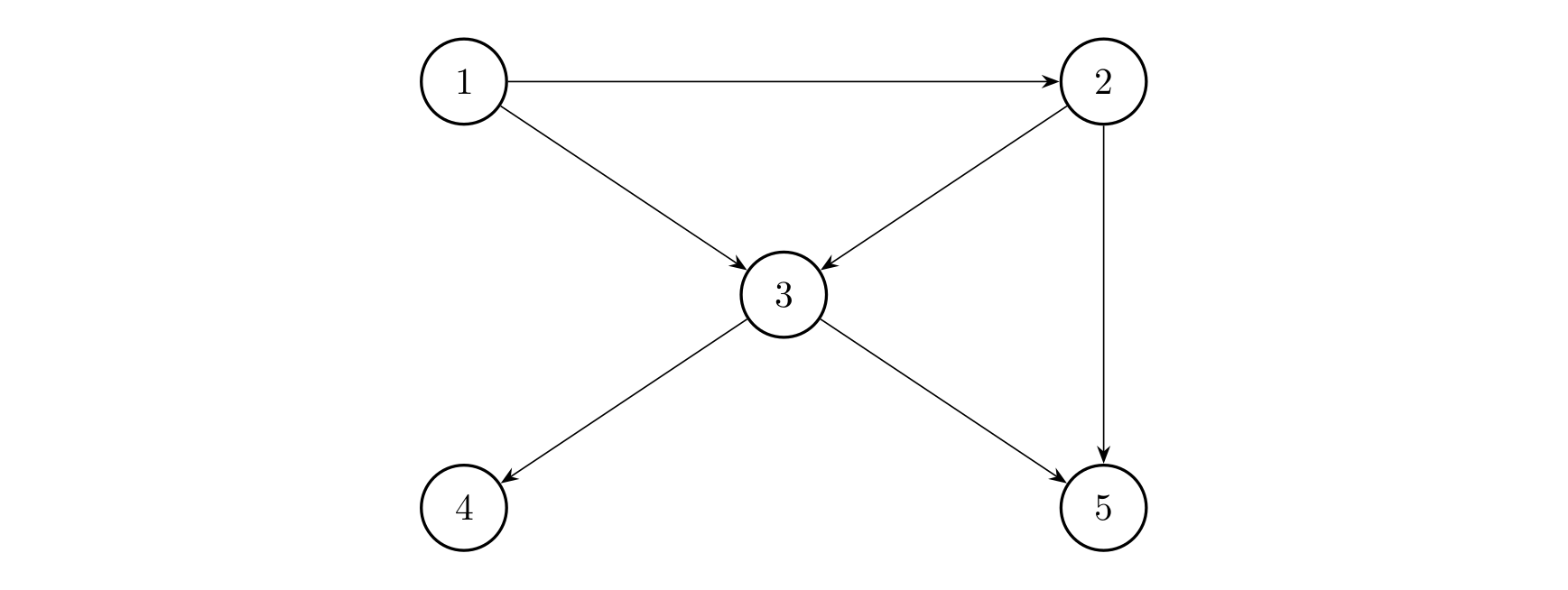
A metric for measuring the connectivity of a directed graph is the reachability count, defined as the number of ordered pairs of vertices in which the second is reachable from the first. As shown in the figure:  Vertex 1 can reach 1, 2, 3, 4, 5. Vertex 2 can reach 2, 3, 4, 5. Vertex 3 can reach 3, 4, 5. Vertices 4 and 5 can only reach themselves. Therefore, the reachability count of this graph is $14$. Given a graph, please compute its reachability count.

The first line contains the number of vertices, a positive integer $N$. Then follow $N$ lines, each containing $N$ characters. In the $i$-th row and $j$-th column, a `1` indicates there is a directed edge from $i$ to $j$, and `0` indicates no edge.

Output a single line with one integer, the reachability count of the graph.

For $100\%$ of the testdata, $1 \le N \le 2000$. Translated by ChatGPT 5