P4337 [ZJOI2018] Line Graph

Jiutiao Kelian is a girl who loves creating problems.

Today, Kelian wants to make a problem related to graph theory. On an undirected graph $G$, we can perform some interesting transformations, such as taking the dual or the complement. These operations often bring new life to classical problems. For example, connectivity of the complement graph and shortest paths on the complement graph are both very interesting problems. Recently, Kelian learned a new transformation: taking the line graph of the original graph. For an undirected graph $G = ⟨V, E⟩$, its line graph $L(G)$ is also an undirected graph: - Its vertex set has size $|E|$, and each vertex corresponds uniquely to an edge of the original graph. 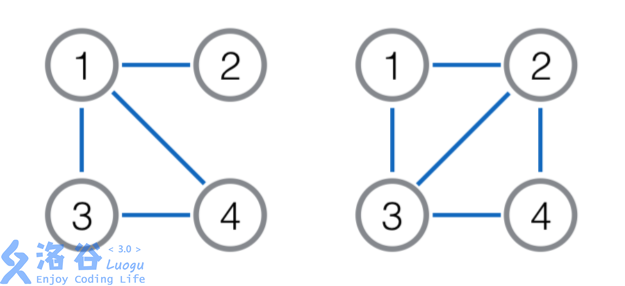- There is an edge between two vertices if and only if the two corresponding edges in the original graph share an endpoint (note that there are no self-loops). The figure below shows a simple example: the left figure is the original graph, and the right figure is its line graph. Vertex $1$ corresponds to edge $(1, 2)$ in the original graph, vertex $2$ corresponds to $(1, 4)$, vertex $3$ corresponds to $(1, 3)$, and vertex $4$ corresponds to $(3, 4)$.  After some initial exploration, Kelian found that the properties of line graphs are much more complicated than those of complement graphs. A notable point is that the complement of the complement returns to the original graph, while $L(L(G))$ is not equal to $G$ in most cases, and in many cases the number of vertices and edges grows rapidly. Therefore, Kelian wants to start from the simplest case, namely computing the number of vertices of $L^k(G)$ (where $L^k(G)$ means taking the line graph of $G$ $k$ times). Unfortunately, even this problem is too hard for her, so she weakens it. She gives a tree $T$ with $n$ nodes and asks you to compute the number of vertices in $L^k(T)$.

The first line contains two integers $n, k$, denoting the number of vertices in the tree and the number of times to take the line graph. The next $n - 1$ lines each contain two integers $u, v$, representing an edge of the tree.

Output a single integer: the answer modulo $998244353$.

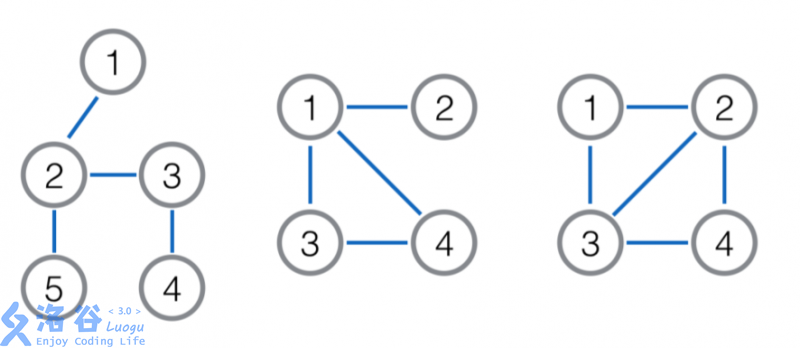
As shown below, the left figure is the original tree, the middle figure is $L(G)$, and the right figure is $L^2(G)$. $L^3(G)$ is not shown here, but since $L^2(G)$ has 5 edges, $L^3(G)$ has 5 vertices.   Translated by ChatGPT 5