P4339 [ZJOI2018] Maze

Kelian is a playful girl.

Summer vacation is coming, and Kelian plans to build a castle next to her private beach so she can invite her friends over during the holidays. She also plans to build a maze under the castle, because exploration is always fun. After a simple design, Kelian plans to build a maze as follows: - The maze can be abstracted as a directed graph with $n$ vertices and $nm$ edges. Vertex $1$ is the only entrance and also the only exit. - Each vertex has exactly $m$ outgoing edges, and these outgoing edges are labeled in order by integers in $[0, m)$. - Self-loops and parallel edges are allowed. A good maze should also have some puzzle elements. Kelian hopes that every cycle starting from vertex $1$ and returning to vertex $1$ follows a certain pattern. She finds that if you record the labels of all edges along a path starting from vertex $1$, you obtain a base-$m$ number (possibly with leading $0$s). Conversely, for every base-$m$ number (possibly with leading $0$s), there exists a corresponding path starting from vertex $1$. Kelian then chooses an integer $K$. She wants the maze to satisfy: a path starting from vertex $1$ returns to vertex $1$ if and only if the number corresponding to this path is a multiple of $K$. Now that $m$ and $K$ have been chosen, she realizes that not every $n$ admits a maze design that meets all the conditions above. Since building a maze is time-consuming and laborious, Kelian wants to find the minimum $n$ that satisfies the conditions. However, Kelian is not interested in complicated calculations, so she asks you to compute this value for her.

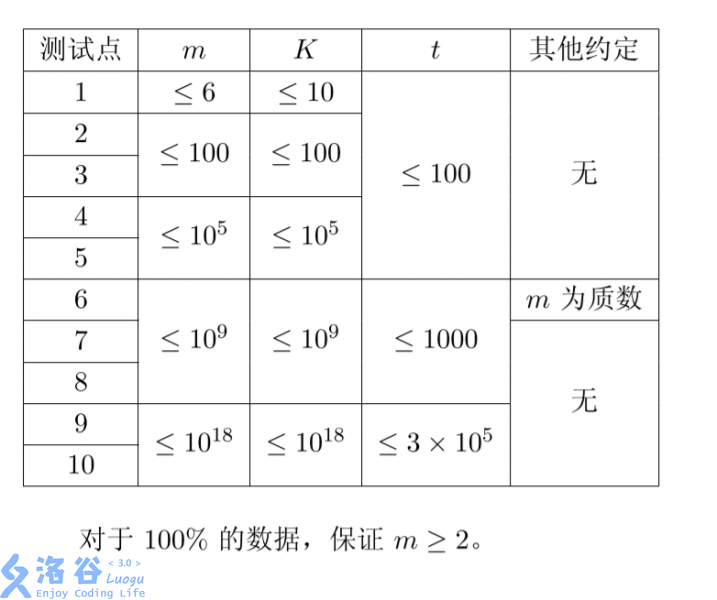
The first line contains an integer $T$ — the number of test cases. Each of the next $T$ lines contains two positive decimal integers $m, K$ — the chosen integers.

For each test case, output a single integer: the minimum $n$ that satisfies all the conditions. If no such $n$ exists, output `-1`.

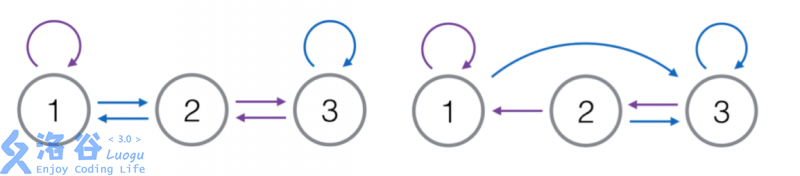
One possible design for the first test case (left) and the second test case (right) is shown below. Purple edges denote the edge labeled $0$, and blue edges denote the edge labeled $1$.   Translated by ChatGPT 5