P4350 [CERC2015] Export Estimate

Luka 经营一家地理数据公司，负责维护详细的城市地图，并将数据导出给有需求的客户。通常客户不需要完整地图，而是希望获得仅包含主要街道的简化地图。

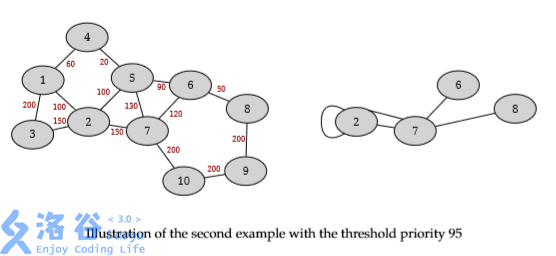
城市地图是一个无向图，包含编号 $1$ 到 $n$ 的 $n$ 个交叉路口和 $m$ 条双向街道。每条街道都有一个非负整数的优先级。当客户请求地图时，会指定一个优先级阈值 $p$。原始地图会经过以下处理流程生成导出地图： 1. 所有优先级小于 $p$ 的街道被删除； 2. 按顺序处理每个交叉路口 $i$（从 $1$ 到 $n$ 依次处理）： (a) 如果这个路口没有连接到任何街道，它就会被删除。 (b) 如果路口 $i$ 恰好连接两条不同街道 $x$ 和 $y$（分别通向不同于 $i$ 的路口 $a$ 和 $b$），则按以下步骤进行收缩： i.删除道路 $x$ 和道路 $y$； ii.删除路口 $i$； iii.加入一条连接路口 $a$ 和 $b$ 的新道路 $z$；  最初，图中没有环（即一条连接到自身的边）或者平行的边（即在同一对交点之间有一条以上的边），但在收缩的过程中可能会形成环和平行边。 请注意，在步骤 2.(b) 之前，$x$ 和 $y$ 都不能是环（即 $a$ 和 $b$ 必须和 $i$ 不同），但是新增的 $z$ 可以是一个环（即 $a$ 和 $b$ 可能是相同的）。 给定地图和一系列导出请求，对每个请求计算导出地图中的路口数量和街道数量。

第一行包含两个整数 $n(1 \le n\le3\times10^5)$ 和 $m(1\le m\le 3\times10^5)$ 分别是点和边的数量。 后面 $m$ 行包含三个整数分别是 $a,b$ 和 $p(1\le a,b \le n,0\le p\le 3\times10^5)$ 用来描述 $a,b$ 之间边的优先级 $p$，没有一条边只连接一个点，两个点之间最多有一条边。 第 $m+2$ 行包含一个整数 $q(1\le q\le 3\times10^5)$ 表示询问的个数，下一行有 $q$ 个整数，第 $k$ 个整数 $t_k(0\le t_k\le 3\times10^5)$ 是第 $k$ 次询问的优先级。

输出包括 $q$ 行。第 $k$ 行包含两个整数，分别是第 $k$ 次询问的点和边的个数。

Central Europe Regional Contest 2015 Problem E