P4362 [NOI2002] The Gluttonous Nine-Headed Dragon

The legendary nine-headed dragon is especially gluttonous. Although it is called a “nine-headed dragon,” that only refers to the fact that it is born with nine heads. During its growth, it may grow many new heads, so the total number of heads can be much larger than nine, and of course some old heads may fall off due to aging.

One day, a nine-headed dragon with $M$ heads sees a fruit tree bearing $N$ fruits. Delighted, it wishes it could eat them all in one bite. However, it must treat each head fairly, so it needs to divide the $N$ fruits into $M$ groups, with at least one fruit in each group, and let each head eat one group. Among these $M$ heads, there is a largest head, called the “Big Head,” which is the leader of the heads. It must eat exactly $K$ fruits, and those $K$ fruits must, of course, include the unique largest fruit. The $N$ fruits are connected by $N-1$ branches. Since the fruit tree is a single connected whole, one can “walk” from any fruit to any other fruit along the branches. For each branch, if the two fruits it connects are to be eaten by different heads, then the two heads will break the branch to separate the fruits. If the two fruits are to be eaten by the same head, then that head will be too lazy to break it and will eat the fruits together with the branch. Eating branches is uncomfortable, so each branch has a “discomfort value,” and the dragon’s total discomfort is the sum of the “discomfort values” of all branches that are eaten by the heads. The dragon wants to minimize its total discomfort. Can you help it compute the minimum? For example, in the instance shown in Figure 1, the fruit tree has $8$ fruits and $7$ branches, with each branch’s “discomfort value” labeled next to it. The dragon has two heads, and the Big Head must eat $4$ fruits, which must include the largest fruit. 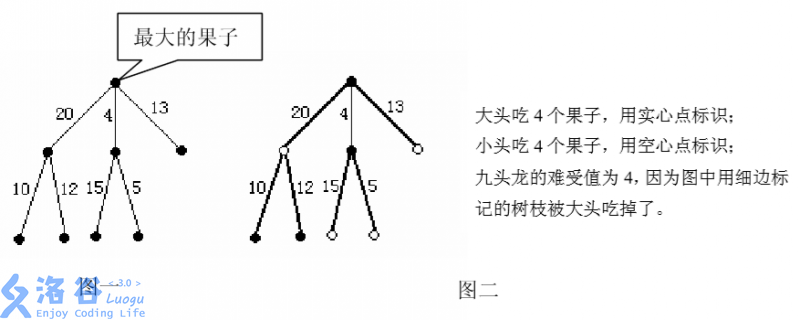That is, $N = 8$, $M = 2$, $K = 4$:  Figure 1 illustrates the shape of the fruit tree, and Figure 2 illustrates the optimal strategy.

The first line contains three integers $N$, $M$, $K$. The $N$ fruits are numbered $1, 2, \cdots, N$, and the largest fruit is always numbered $1$. Lines $2$ through $N$ describe the structure of the fruit tree. Each line contains three integers $a, b, c$, indicating that there is a branch with discomfort value $c$ connecting fruits $a$ and $b$.

Output a single line containing one integer, the minimum possible total discomfort while satisfying the Big Head’s requirement. If it is impossible to meet the requirement, output $-1$.

This sample corresponds to the example in the problem statement. Constraints For $100\%$ of the testdata, $1 \le N \le 300$, $2 \le M \le N$, $1 \le K \le N$, $1 \le a, b \le N$, $0 \le c \le 10^5$. Translated by ChatGPT 5