P4363 [Nine-Province Joint Exam 2018] Double Wooden Chess (chess)

Feifei and Niuniu play on an $n$ by $m$ board. Feifei plays black and goes first, Niuniu plays white and goes second. At the start, the board is empty. They alternately place pieces on cells until the board is completely filled. The placement rule is: a cell can be chosen if and only if the cell is empty and all cells to its left in the same row and all cells above it in the same column already contain pieces. Each cell of the board has two nonnegative integers written on it. For the cell in row $i$ (from top to bottom) and column $j$ (from left to right), the two integers are denoted by $a_{i, j}$ and $b_{i, j}$. After the game ends, Feifei’s score is the sum of $a_{i, j}$ over all cells with a black piece, and Niuniu’s score is the sum of $b_{i, j}$ over all cells with a white piece. Both players want to maximize the result of their own score minus the opponent’s score. They would like to know, on the given board, if both sides play optimally and know the other will also play optimally, what is the final result.

The first line contains two integers, the numbers of rows $n$ and columns $m$ of the board. Lines $2$ through $(n + 1)$ each contain $m$ integers; on line $(i + 1)$, the $j$-th integer is $a_{i, j}$. Lines $(n + 2)$ through $(2n + 1)$ each contain $m$ integers; on line $(n + i + 1)$, the $j$-th integer is $b_{i, j}$.

Output a single integer, the value of Feifei’s score minus Niuniu’s score.

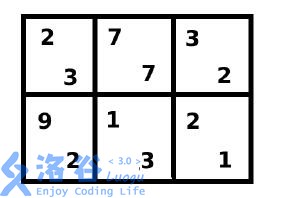
### Sample 1 Explanation  The board is as shown. Under optimal play, the game proceeds as follows: - Feifei plays at row $1$, column $1$ (this is the only legal move on the first turn). - Niuniu plays at row $1$, column $2$. - Feifei plays at row $2$, column $1$. - Niuniu plays at row $1$, column $3$. - Feifei plays at row $2$, column $2$. - Niuniu plays at row $2$, column $3$ (this is the only legal move on this turn). - The board is filled, and the game ends. 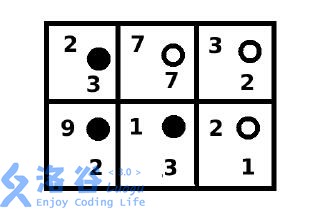The final position is:  Feifei’s score is $2 + 9 + 1 = 12$, and Niuniu’s score is $7 + 2 + 1 = 10$. ### Constraints The information for each test point is shown in the table below.  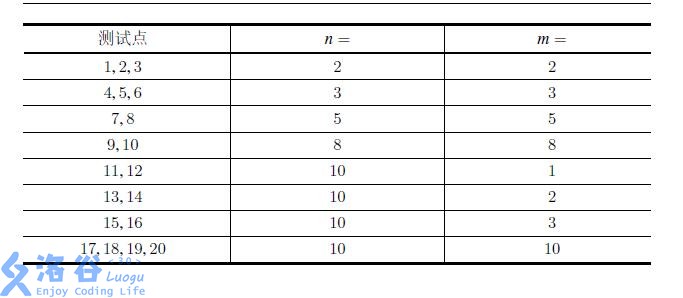- For test points with odd indices, it is guaranteed that $b_{i, j} = 0$. - For all test points, it is guaranteed that $1 \leq n, m \leq 10$ and $0 \leq a_{i, j}, b_{i, j} \leq 10^5$. Translated by ChatGPT 5