P4365 [Nine-Province Joint Exam 2018] Secret Raid coat
Background
> We could have had it all. . . . . .
>
> 我们本该,拥有一切
>
> Counting on a tree. . . . . .
>
> 何至于此,数数树上
Counting on a Tree (CoaT) is the English name of this problem.
Description
Access Globe is playing a strategy game. In the game, he controls a soldier from country C. His mission is to follow the commander’s orders to join battles and win.
Country C is about to launch a secret raid on country D. The battle plan is: choose $s$ cities in country D, and send the $s$ top-performing soldiers of country C to secretly infiltrate these cities, one soldier per city. Each city has a danger level $d_i$.
The commander of country C will send the best-performing soldier to the most dangerous city among the chosen cities, the second-best to the second most dangerous city, and so on (that is, the soldier with the $i$-th highest record goes to the city with the $i$-th highest danger level among the chosen cities). Country D has $n$ cities, with $n - 1$ bidirectional roads connecting them, so that every pair of cities is mutually reachable. To ensure smooth execution, among the $s$ chosen cities, any two chosen cities can reach each other without passing through any unchosen city.
Access Globe controls the soldier with the $k$-th highest record, and he wants to estimate the danger level of the city he will eventually infiltrate. He assumes country C chooses any set $S$ of cities that satisfies the conditions uniformly at random. He wants you to compute, over all possible city sets, the sum of the danger levels of the city that Access Globe’s soldier will infiltrate. If fewer than $k$ cities are chosen, Access Globe will not be dispatched; in this case the danger level is $0$.
Of course, you do not want to solve this problem for him, and you are not going to tell him the remainder modulo $998\,244\,353$. You will only tell him the remainder modulo $64\,123$.
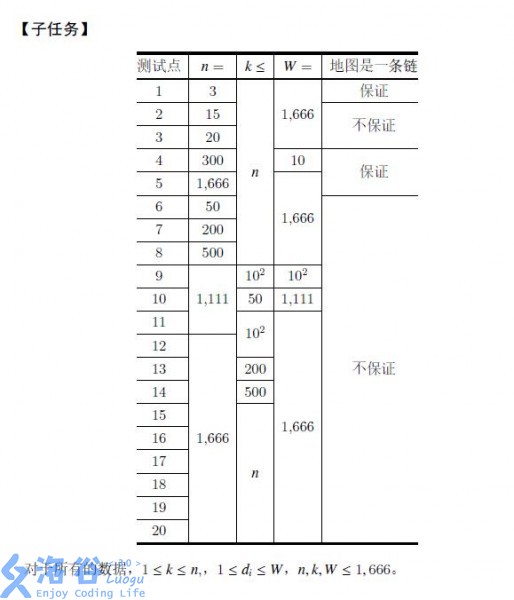
Input Format
The first line contains $3$ integers $n, k, W$, denoting the number of cities in country D, the rank of the city that Access Globe’s soldier will infiltrate, and the maximum danger level among all cities in country D.
The second line contains $n$ integers between $1$ and $W$, $d_1, d_2, \ldots, d_n$, denoting the danger level of each city.
Lines $3$ through $n + 1$ each contain two integers $x_i, y_i$, indicating that there is a bidirectional road between cities $x_i$ and $y_i$ in country D.
Output Format
Output a single integer: the remainder modulo $64\,123$ of the sum, over all feasible city sets, of the danger level of the city that Access Globe’s soldier will infiltrate.
Explanation/Hint
Country D’s map is shown below. A city with danger level $d$ is drawn as a $(d + 3)$-gon.
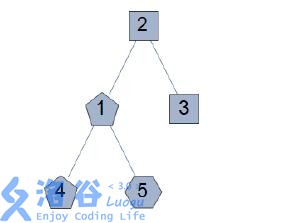
All valid choices with at least $3$ selected cities are:
- Choose cities $1, 2, 3$; the danger level for Access Globe’s soldier is $1$.
- Choose cities $1, 2, 3, 4$; the danger level is $1$.
- Choose cities $1, 2, 3, 5$; the danger level is $1$.
- Choose cities $1, 2, 3, 4, 5$; the danger level is $2$.
- Choose cities $1, 2, 4$; the danger level is $1$.
- Choose cities $1, 2, 5$; the danger level is $1$.
- Choose cities $1, 2, 4, 5$; the danger level is $2$.
- Choose cities $1, 4, 5$; the danger level is $2$.
- When fewer than $3$ cities are chosen, the danger level is $0$.
Therefore you should output $(1 + 1 + 1 + 2 + 1 + 1 + 2 + 2) \bmod 64\,123 = 11$.
Translated by ChatGPT 5