P4367 [Code+#4] Tommy's Bonding

The deep sky seems to devour everything; a Codeforces contest has just ended. “Why are you still ignoring me...”, sleepy-eyed Tommy picks up the phone lying beside him. The empty QQ notification box carries no warmth. Tommy sighs. The dim lamp glows faintly, brushing over the humming computer. The desk is piled with scratch paper full of $\partial$ and $\int$. The phone’s flashlight, a makeshift desk lamp, emits dazzling white light; the flickering lights reflect a painted, weary face. A dozen DDLs are around the corner, and the person on the other end of QQ hasn’t slept for three days and nights. This is what Tommy doesn’t know.

Life is probably like this. In this materialistic world, people hustle for a living, talk less and less, and grow more distant emotionally. However, the latest research by the renowned scientist Access Globe can solve this: increase the shared topics by increasing the things done simultaneously. A and B each receive some tasks. Let the sets of tasks they need to execute be $V_A$ and $V_B$, respectively. For each person, task $1$ must be done first, and each other task $e$ has a prerequisite task $p_e$, meaning task $e$ can be executed only after $p_e$ is completed. That is, the dependency of each person’s tasks forms a rooted directed tree whose edges point away from the root. A task $e$ can be executed if and only if all tasks $p_e, p_{p_e}, \cdots, 1$ have been executed. We say task $e$ depends on tasks $p_e, p_{p_e}, \cdots, 1$. Now, A and B hope to complete some tasks together, so they decide to select tasks as follows: A selects $m$ tasks $a_1, \cdots, a_m$ with the requirements $a_1 = 1$ and, for any $1 \le i < m$, task $a_{i+1}$ depends on $a_i$. Similarly, B selects $m$ tasks $b_1, \cdots, b_m$ satisfying the same requirements. Then A can execute tasks along the path from $1$ to $a_m$ in order, and B can execute tasks along the path from $1$ to $b_m$ in order. Moreover, after scheduling, when A is executing task $a_i$, B is executing task $b_i$ at the same time. At such moments, A and B can get in touch and increase their intimacy. The objective is to maximize the intimacy. For each pair of simultaneously executed tasks $a_i$ and $b_i$, they gain a score of $C_{a_i, b_i}$. Meanwhile, once A and B lose contact, their intimacy decreases: in each minute, if it is the $i$-th minute since one side last contacted the other, the intimacy decreases by $2i - 1$. For example, suppose the times for the two people’s tasks are 2, 1, 4, 7 and 4, 8, 3, 6, 4, and they jointly complete only the first and the last tasks. Then A has 1 + 4 = 5 minutes without contact while executing the two middle tasks, which causes an intimacy decrease of $1 + 3 + \cdots + 11 = 25$; B has 8 + 3 + 6 = 17 minutes without contact while executing the three middle tasks, which causes an intimacy decrease of $1 + 3 + \cdots + 35 = 289$. Note that the intimacy calculation depends only on task execution times, and any two tasks can be executed simultaneously as $a_i$ and $b_i$; they need not take the same amount of time. Given A’s and B’s tasks, dependencies, and the execution time of each task, please compute the maximum intimacy that can be achieved.

Read from standard input. - The first line contains two integers $|V_A|, |V_B|$. - The second line contains $|V_A| - 1$ integers $t^{(a)}_{2}, t^{(a)}_{3}, \ldots, t^{(a)}_{|V_A|}$, the duration of each of A’s tasks. - The third line contains $|V_B| - 1$ integers $t^{(b)}_{2}, t^{(b)}_{3}, \ldots, t^{(b)}_{|V_B|}$, the duration of each of B’s tasks. - The fourth line contains $|V_A| - 1$ integers $p^{(a)}_{2}, p^{(a)}_{3}, \ldots, p^{(a)}_{|V_A|}$, the prerequisite of each of A’s tasks, with $p^{(a)}_{i} < i$ guaranteed. - The fifth line contains $|V_B| - 1$ integers $p^{(b)}_{2}, p^{(b)}_{3}, \ldots, p^{(b)}_{|V_B|}$, the prerequisite of each of B’s tasks, with $p^{(b)}_{i} < i$ guaranteed. - Then follow $|V_A| - 1$ lines, each with $|V_B| - 1$ integers. In the $(i - 1)$-th row and $(j - 1)$-th column is $C_{i, j}$, the intimacy gained if A and B simultaneously execute tasks $i$ and $j$, respectively. Note that these intimacy scores are not necessarily nonnegative. Note: the above input does not include information for task $1$, because it is irrelevant to the intimacy calculation.

Output to standard output. Print the maximum achievable intimacy.

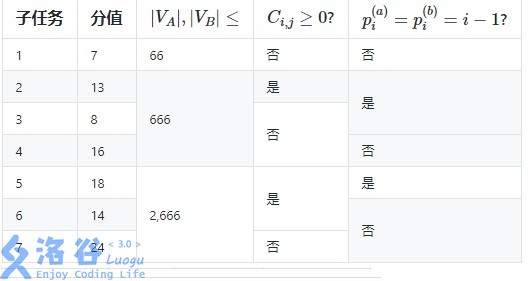
Sample explanation: A and B select tasks $1, 3, 4$ and $1, 2, 3$, respectively. The simultaneous pairs $(1, 1)$, $(3, 2)$, and $(4, 3)$ yield intimacy $4 + 5 = 9$. A executes task $2$ alone for 2 minutes and loses $1 + 3 = 4$ intimacy. Therefore, the final total intimacy is $9 - 4 = 5$. This is the optimal plan.  Constraints: For all testdata, $2 \le |V_A|, |V_B| \le 2{,}666$, $1 \le t^{(a)}_i, t^{(b)}_i \le 1{,}206$, and $0 \le |C_{i, j}| \le 2{,}017{,}011{,}328$. Credit: https://www.luogu.org/discuss/show/38908 Credit: idea and problemsetting/Chen Junkun; problem verification/Tommy > < Git Repo: https://git.thusaac.org/publish/CodePlus4 Thanks to Tencent for supporting this contest. Translated by ChatGPT 5