P4371 [Code+#4] Platinum Head of State and Seven-Color Magic

Children, how are you? Do you still remember who I am? I am the magical head of state Madoka!

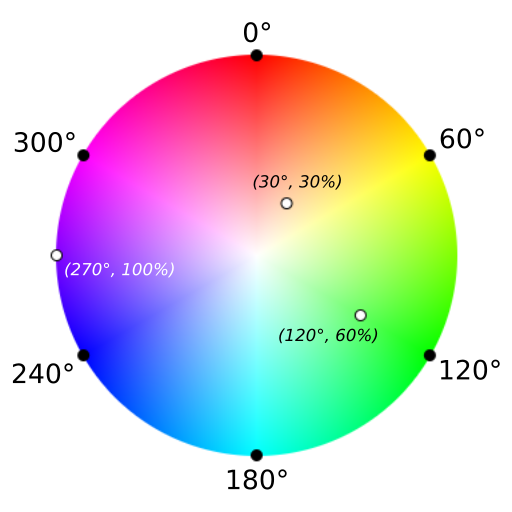
"Make a contract with me and become a magical head of state!" On this day, the head of state was coaxed by the extraterrestrial creature Kyubey into becoming a magical head of state. However, before practicing magic, the head of state needs to choose a representative color for their magic. The figure below is a unit-circle color wheel with maximum value (that is, in the HSV color space, $V = 100\%$). The coordinates of any point on the wheel are a pair of nonnegative real numbers $(\alpha^\circ, r\%)$ ($0 \leq \alpha < 360, 0 \leq r \leq 100$), meaning a color with hue $\alpha^\circ$ and saturation $r\%$. Another interpretation is that $\alpha^\circ$ is the angle swept clockwise from the ray connecting the center of the circle to the pure red point to the given point, and $\frac{r}{100}$ is the distance from that point to the center of the unit circle.  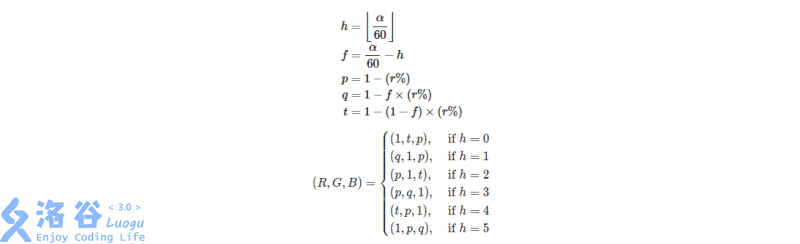Specifically, the conversion from these coordinates $(\alpha^\circ, r\%)$ to RGB values $(R, G, B)$ is as follows:  Please refer to the sample to confirm your understanding and implementation of the formula. According to Kyubey, the head of state may choose any color on a given line segment $(\alpha_1^\circ, r_1\%)-(\alpha_2^\circ, r_2\%)$ lying on the plane of the color wheel. No need to hesitate—being a bling bling imperial leader, of course they will choose the brightest color! The brightness of a color $(R, G, B)$ is defined as $L = 0.30R + 0.59G + 0.11B$. The figure below shows a side-by-side comparison between the colorful color wheel and a grayscale wheel representing brightness.  You need to write a program to compute the maximum brightness among all colors on the given line segment.

Read from standard input. The first line contains a positive integer $T$ — the number of test cases. Then follow $T$ test cases with no blank lines between them. Line 1: Four space-separated integers $\alpha_1$, $r_1$, $\alpha_2$, $r_2$.

Output to standard output. For each test case, output one line containing a decimal in the range $[0, 1]$ — the maximum brightness among all colors on the line segment $(\alpha_1^\circ, r_1\%)-(\alpha_2^\circ, r_2\%)$, rounded to exactly four decimal places. It is guaranteed that if the reference answer is $A$, then any real number in the range $[A - 10^{-5}, A + 10^{-5}]$ will round to the same value at four decimal places.

Sample explanation: The point $(30^\circ, 30\%)$ has RGB values $(1.00, 0.85, 0.70)$, with brightness $0.30 \times 1.00 + 0.59 \times 0.85 + 0.11 \times 0.70 = 0.8785$. The point $(120^\circ, 60\%)$ has RGB values $(0.40, 1.00, 0.40)$, with brightness $0.30 \times 0.40 + 0.59 \times 1.00 + 0.11 \times 0.40 = 0.7540$. The point $(270^\circ, 100\%)$ has RGB values $(0.50, 0.00, 1.00)$, with brightness $0.30 \times 0.50 + 0.59 \times 0.00 + 0.11 \times 1.00 = 0.2600$.  "Ich glaube, ich habe mich klar genug ausgedrückt!" This statement has nothing to do with historical facts. Credit: https://www.luogu.org/discuss/show/38908 Translated by ChatGPT 5