P4381 [IOI 2008] Island

You plan to tour a park that consists of $N$ islands. From each island $i$, the local authority has built a bridge to another island, with length $L_i$, and bridges can be walked in both directions. In addition, for every pair of islands there is a dedicated ferry that connects the two. Compared with taking a ferry, you prefer walking. You want the total length of bridges you walk across to be as large as possible, subject to the following rules: - You may choose any island to start your tour. - No island may be visited more than once. - At any time, you may move from your current island $S$ to another unvisited island $D$. You may do so in one of the following ways: - Walk: only if there is a bridge directly between the two islands. In this case, the bridge length is added to your total walking distance. - Ferry: you may choose this only if there is no combination of bridges and ferries you have already used that allows you to get from $S$ to $D$. When checking reachability, you should consider all paths, including those that pass through islands you have already visited. Note that you do not have to visit all the islands, and you might be unable to walk across all the bridges. Write a program that, given $N$ bridges and their lengths, computes the maximum possible sum of bridge lengths you can walk under the rules above.

The first line contains an integer $N$, the number of islands in the park. Each of the next $N$ lines describes one island. The $i$-th line contains two integers, separated by a single space, describing the bridge built from island $i$: the first integer is the other endpoint island, and the second integer is the bridge length $L_i$. You may assume that the endpoints of every bridge are always different islands.

Output a single integer, the maximum possible walking distance.

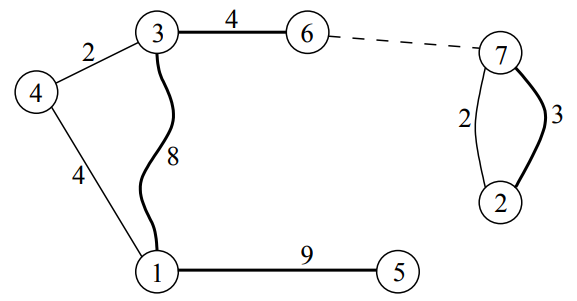
Sample explanation:  In the sample, $N=7$ bridges are $(1-3)$, $(2-7)$, $(3-4)$, $(4-1)$, $(5-1)$, $(6-3)$, and $(7-2)$. Note that there are two different bridges between islands $2$ and $7$. One way to achieve the maximum walking distance is as follows: - Start at island $5$. - Walk across the bridge of length $9$ to island $1$. - Walk across the bridge of length $8$ to island $3$. - Walk across the bridge of length $4$ to island $6$. - Take the ferry from island $6$ to island $7$. - Walk across the bridge of length $3$ to island $2$. You end at island $2$, and your total walking distance is $9+8+4+3=24$. Only island $4$ is not visited. Note that, at the end of the tour above, you cannot visit that island. More precisely: - You cannot walk there because there is no bridge between island $2$ (your current island) and island $4$. - You cannot take a ferry there because island $4$ is reachable from your current island $2$. One possible way is: take bridge $(2-7)$, then the previously used ferry from island $7$ to island $6$, then take bridge $(6-3)$, and finally bridge $(3-4)$. Constraints: For $100\%$ of the testdata, $2 \leqslant N \leqslant 10^6$, $1 \leqslant L_i \leqslant 10^8$. Translated by ChatGPT 5