P4382 [Eight-Province Joint Exam 2018] Pi Pei

The annual variety show "China's New Code" has begun again. Zayid has dreamed of becoming a programmer since childhood. He feels this is a stage to show himself, so he signed up without hesitation.

Skilled as usual, Zayid smoothly passed the open auditions. The next stage is the mentors' blind selection, with rules as follows: There are $n$ contestants in total (numbered from $1$ to $n$). Each writes a piece of code and presents their dream. Then all mentors rank these contestants. To avoid future trouble, it is required that there are no ties in the rankings. At the same time, each contestant independently fills out a preference form to evaluate the $m$ mentors (numbered from $1$ to $m$). The form contains $m$ preference tiers. For each tier, the contestant may list at most $C$ mentors, and each mentor may be listed at most once by each contestant (skipping some mentors is allowed). After both sides finish, admissions are carried out. Each mentor has an upper bound on their team size, which means some contestants' higher preferences, or even all their preferences, may not be met. The show defines "the result for the top $i$ contestants is optimal" as follows: - The result for the top $1$ contestant is optimal if and only if contestant $1$ is admitted to their highest nonempty preference (in particular, if contestant $1$ did not submit a preference form, then this contestant is eliminated). - The result for the top $i$ contestants is optimal if and only if, given that the result for the top $i - 1$ contestants is optimal, contestant $i$ is admitted to the highest preference that is theoretically possible (in particular, if contestant $i$ did not submit a preference form, or if all mentors in their preferences are already full, then this contestant is eliminated). If a scheme satisfies "the result for the top $n$ contestants is optimal," we simply call this scheme optimal. For example, there are $2$ mentors, Teacher $\rm T$ and Teacher $\rm F$, each with a team size cap of $1$; there are $2$ contestants, Zayid and DuckD, ranked $1$ and $2$, respectively. 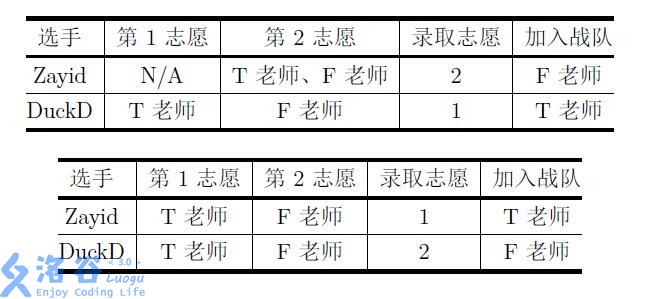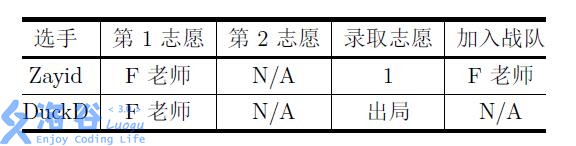Then the following $3$ preference forms and their corresponding optimal admission results are as shown in the tables:   It can be proved that, for the above preference forms, the corresponding schemes are the unique optimal admission results. Everyone has an ideal value $s_i$, meaning that contestant $i$ hopes to be admitted to their $s_i$-th or better preference; otherwise, they will be very disappointed. Now all contestants' preference forms and rankings have been published. Coincidentally, each contestant's ranking exactly matches their ID. For each contestant, Zayid wants to know the answers to the following two questions: - In the optimal admission scheme, to which preference tier will they be admitted? - With other contestants' relative order unchanged, by at least how many ranks must they climb so that they are not disappointed? As a top-notch coder on "China's New Code," Zayid certainly solved this problem easily. But he still wants you to compute it again to verify his result.

Each test point contains multiple testcases. The first line contains $2$ non-negative integers $T, C$ separated by a space, representing the number of testcases and the maximum number of mentors allowed per preference tier, respectively. Then for each testcase: - The first line contains two positive integers $n, m$ separated by a space. > $n, m$ denote the number of contestants and the number of mentors, respectively. - The second line contains $m$ positive integers separated by spaces: the $i$-th integer is $b_i$. > $b_i$ is the team size upper bound of mentor $i$. Lines $3$ to $n + 2$ each contain $m$ non-negative integers: in line $i + 2$, the $j$-th number from the left is $a_{i,j}$. > $a_{i,j}$ means contestant $i$ placed mentor $j$ as their $a_{i,j}$-th preference. In particular, if $a_{i,j} = 0$, it means this contestant did not include this mentor on the form. > In this part, it is guaranteed that within each row no positive number appears more than $C$ times ($0$ may appear more than $C$ times), and all $a_{i,j} \leqslant m$. - Line $n + 3$ contains $n$ positive integers separated by spaces, where the $i$-th integer is $s_i$. > $s_i$ is the ideal value of contestant $i$. > In this part, it is guaranteed that $s_i \leqslant m$.

Output the answers for each testcase in order. For each testcase, output $2$ lines: - The first line contains $n$ positive integers separated by spaces. The $i$-th integer means: the preference tier to which contestant $i$ will be admitted in the optimal scheme. > In particular, if this contestant is eliminated, this number is $m + 1$. - The second line contains $n$ non-negative integers separated by spaces. The $i$-th integer means: the minimum number of ranks contestant $i$ must climb so as not to be disappointed. > In particular, if this contestant will certainly be disappointed, this number is $i$.

- Explanation for Sample $1$: The three datasets correspond to the three tables in the Description. For the first dataset: because contestant $1$ did not list any first preference, they definitely cannot be admitted to their first preference tier and will definitely be disappointed. Contestant $2$ is not disappointed with the original ranking, so they do not need to improve their rank. For the second and third datasets: contestant $1$ does not need to improve their rank. Aiming for first preference, contestant $2$ must rise to rank $1$ to get their wish. - Explanation for Sample $2$: Contestant $1$ listed only mentor $2$ as first preference, so contestant $1$ must be admitted by mentor $2$. Contestant $2$ listed only mentor $3$ as first preference, so contestant $2$ must be admitted by mentor $3$. Since mentors $2$ and $3$ are full, and contestants $3$ and $4$ both listed mentor $1$, they will both be admitted by mentor $1$. Therefore, contestants $1$ and $2$ are both admitted to their $1$-st preference, contestant $3$ is admitted to their $3$-rd preference, and contestant $4$ is admitted to their $2$-nd preference. Since they all get what they want, none of them needs to improve their rank. | Test point ID | $n \leqslant$ | $m \leqslant$ | $C$ | Other conditions | |:----:|:---:|:----:|:----:|:----:| | 1 | $10$ | $1$ | $=1$ | None | | 2 | $10$ | $2$ | $=2$ | $s_i = m$ | | 3 | $10$ | $3$ | $=3$ | None | | 4 | $100$ | $100$ | $=1$ | $b_i = 1$ | | 5 | $100$ | $100$ | $=1$ | None | | 6 | $200$ | $200$ | $=1$ | $b_i = 1$ | | 7 | $200$ | $200$ | $=1$ | None | | 8 | $100$ | $100$ | $=10$ | None | | 9 | $200$ | $200$ | $=10$ | $b_i = 1$ | | 10 | $200$ | $200$ | $=10$ | None | - For all test points, it is guaranteed that $T \leqslant 5$. - Across all data of all test points, it is guaranteed that $m \leqslant n \leqslant 200, b_i \leqslant n$. Translated by ChatGPT 5