P4426 [HNOI/AHOI2018] Duliu

There was once a "Duliu" (pinyin). Duliu recently discovered the secret to mass-producing "duliu" problems. Consider a data-structure problem of the following type: given an array, you need to support several quirky update operations (for example, adding a number to a range, or taking the square root on a range), and support querying range sums. Duliu considered $n$ such update operations, numbered $1\sim n$. When Duliu wants to set a data-structure problem, he selects some of these update operations and turns them into a problem. Of course, such a problem might be unsolvable. Through clever mathematical reasoning, Duliu revealed the relationships among these update operations: there are $m$ pairs of mutually exclusive update operations, and the $i$-th pair is the $u_i$-th operation and the $v_i$-th operation. When a problem contains both $u_i$ and $v_i$, the problem becomes unsolvable. On the other hand, if a problem contains no mutually exclusive pairs, then the problem is solvable. In addition, Duliu discovered a pattern: $m-n$ is a small number, and any two update operations are connected. Two update operations $a, b$ are connected if and only if there exist operations $t_0, t_1, \cdots, t_l$ such that $t_0 = a$, $t_l = b$, and for $1 \le i \le l$, $t_{i-1}$ and $t_i$ are mutually exclusive. A pair of mutually exclusive update operations is called an exclusive pair. Now Duliu wants to know, given $n$ and the $m$ exclusive pairs, how many different solvable data-structure problems he can set. Two data-structure problems are different if and only if there exists an update operation that appears in one but not in the other.

The first line contains positive integers $n, m$. The next $m$ lines each contain two positive integers $u, v$, representing a pair of mutually exclusive update operations.

Output a single integer on one line, representing the number of solvable different data-structure problems that Duliu can set. This number can be large, so output it modulo $998244353$.

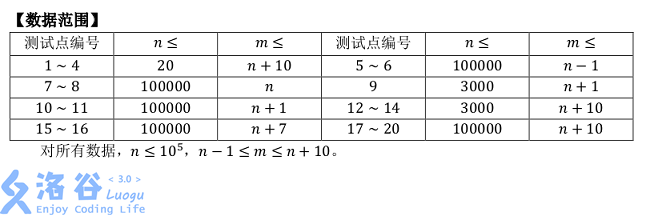
#### Explanation for Sample 1 The solvable problems include $\varnothing, \{1\}, \{2\}, \{3\}, \{1, 3\}$. Note that the empty set is a valid data-structure problem. #### Constraints  Translated by ChatGPT 5