P4438 [HNOI/AHOI2018] Roads

The transportation network of Country W forms a tree. There are $n - 1$ cities and $n$ villages in total; cities are numbered $1$ to $n - 1$, villages are numbered $1$ to $n$, and city $1$ is the capital. All roads are one-way; in this problem we only consider the road network from villages towards the capital. For each city, there is exactly one highway and one railway leading into this city. For city $i$, the starting point of a road (highway or railway) that leads to city $i$ is either a village, or a city whose index is greater than $i$. No roads lead into any village. Except for the capital, every city or village has exactly one outgoing road; the capital has no outgoing road. Starting from any village and following the unique outgoing road, you will eventually reach the capital. King W of Country W has obtained some funds to improve transportation. Due to limited funds, he can renovate $n - 1$ roads. He will renovate exactly one incoming road for each city, i.e., for each city he chooses either its highway or its railway to renovate. To make travel from villages to the capital as convenient as possible, based on census data he sets three parameters for each village. For village $i$, the parameters are $a_i$, $b_i$, and $c_i$. Suppose that starting from village $i$ and going to the capital, you pass through $x$ unrenovated highways and $y$ unrenovated railways. Then the inconvenience value of this village is: $$c_i \cdot (a_i + x) \cdot (b_i + y)$$ Under a given renovation plan, the sum of inconvenience values over all villages is the inconvenience value of that plan. Among all ways to renovate $n - 1$ roads, the plan with the minimum total inconvenience is called the optimal renovation plan. King W wants this optimal plan. Please compute the total inconvenience of the optimal renovation plan.

The first line contains a positive integer $n$. The next $n - 1$ lines each describe a city. The $i$-th of these lines contains two numbers $s_i, t_i$. Here $s_i$ is the starting point of the highway that leads to city $i$, and $t_i$ is the starting point of the railway that leads to city $i$. If $s_i > 0$, then there is a highway from city $s_i$ to city $i$; otherwise there is a highway from village $-s_i$ to city $i$. Similarly, if $t_i > 0$, then there is a railway from city $t_i$ to city $i$; otherwise there is a railway from village $-t_i$ to city $i$. The next $n$ lines each describe a village. The $i$-th of these lines contains three numbers $a_i, b_i, c_i$, as defined above.

Output one line with a single integer: the total inconvenience of the optimal renovation plan.

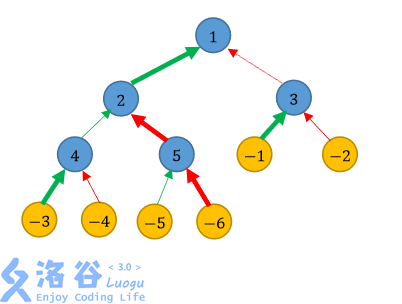
Sample Explanation 1.  In the figure, blue and yellow nodes denote cities and villages, respectively; green and red arrows denote highways and railways, respectively; bold arrows denote renovated roads. One plan with total inconvenience equal to $54$ is: renovate the railways leading to city $2$ and city $5$, and renovate the highways leading to all other cities. Using $\rightarrow$ and $\Rightarrow$ to denote highway and railway, and $∗\rightarrow$ and $∗\Rightarrow$ to denote renovated highway and renovated railway, respectively, we have: The route for village $1$ to reach the capital is: $-1 ∗\rightarrow 3 \Rightarrow 1$, passing $0$ unrenovated highways and $1$ unrenovated railway, with cost $3 \times (1 + 0) \times (2 + 1) = 9$. The route for village $2$ to reach the capital is: $-2 \Rightarrow 3 \Rightarrow 1$, passing $0$ unrenovated highways and $2$ unrenovated railways, with cost $2 \times (1 + 0) \times (3 + 2) = 10$. The route for village $3$ to reach the capital is: $-3 ∗\rightarrow 4 \rightarrow 2 ∗\rightarrow 1$, passing $1$ unrenovated highway and $0$ unrenovated railways, with cost $3 \times (2 + 1) \times (1 + 0) = 9$. The route for village $4$ to reach the capital is: $-4 \Rightarrow 4 \rightarrow 2 ∗\rightarrow 1$, passing $1$ unrenovated highway and $1$ unrenovated railway, with cost $1 \times (2 + 1) \times (3 + 1) = 12$. The route for village $5$ to reach the capital is: $-5 \rightarrow 5 ∗\Rightarrow 2 ∗\rightarrow 1$, passing $1$ unrenovated highway and $0$ unrenovated railways, with cost $2 \times (3 + 1) \times (1 + 0) = 8$. The route for village $6$ to reach the capital is: $-6 ∗\Rightarrow 5 ∗\Rightarrow 2 ∗\rightarrow 1$, passing $0$ unrenovated highways and $0$ unrenovated railways, with cost $1 \times (3 + 0) \times (2 + 0) = 6$. The total inconvenience is $9 + 10 + 9 + 12 + 8 + 6 = 54$. It can be proven that this is the optimal answer for this testdata. Sample Explanation 2. In this sample, it is obvious that all highways should be renovated. Constraints - There are in total $20$ sets of testdata, numbered $1$ to $20$. - For sets with index $\le 4$, $n \le 20$. - For sets with index $5 \sim 8$, $a_i, b_i, c_i \le 5$, $n \le 50$. - For sets with index $9 \sim 12$, $n \le 2000$. - For all sets, $n \le 20000$, $1 \le a_i, b_i \le 60$, $1 \le c_i \le 10^9$, $s_i, t_i$ are integers in $[-n, -1] \cup (i, n - 1]$, and from any village the capital is reachable via no more than $40$ roads. Translated by ChatGPT 5