P4455 [CQOI2018] Social Network

In today's society, checking friends' posts on social networks has become part of many people's lives. Usually, after a user posts a message on a social network, their friends can also see it and may forward it. The forwarded message can continue to be forwarded, spreading through the entire social network.

In a small experimental social network, we found that sometimes a popular message is eventually forwarded by everyone. To study how this happens, we want to compute how many possible forwarding paths there are for a single message. For convenience, we number the initial sender as user $1$, and number the other users in increasing order. All friend relations on this social network are known. That is, for two users $a$ and $b$, we know that user $a$ can see messages sent by user $b$. Note that one-way friend relations may exist; that is, $a$ can see $b$'s messages, but $b$ cannot see $a$'s. Another assumption is that if a user sees that multiple friends forwarded the same message, they will choose exactly one of them to forward from, and will forward at most once. Forwarding from different friends is considered different cases. If we use arrows to represent friend relations, the figures below show all possible forwarding situations in a certain social network. 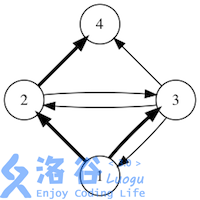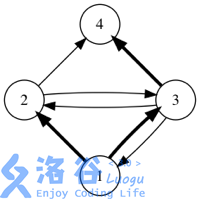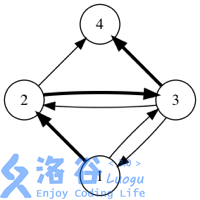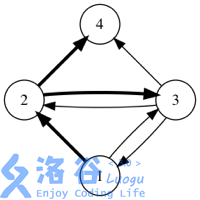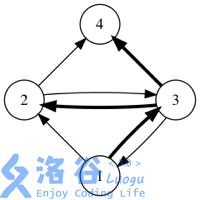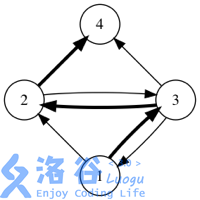(The initial message is sent by user $1$, and bold arrows indicate a single forwarding.)       Output the answer modulo $10^4 + 7$.

The first line contains an integer $n$, the number of users. The second line contains an integer $m$, the number of friend relations. Each of the next $m$ lines contains two integers $a, b$, indicating a friend relation, i.e., user $a$ can see messages sent by user $b$.

Output a single line with one integer: the answer modulo $10^4 + 7$.

Constraints: - For $30\%$ of the testdata, $n \leq 10$. - For $100\%$ of the testdata, $1 \leq n \leq 250$, $1 \leq m \leq n \times (n - 1)$, $1 \leq a, b \leq n$. Translated by ChatGPT 5