P4458 [BJOI2018] Quadratic Sum on a Chain

There is a chain of length $n$ (an undirected graph where $\forall 1 \leq i < n$, there is an edge between node $i$ and node $i+1$). Each node has an integer weight; the weight of the $i$-th node is $a_i$. There are $m$ operations, each as follows: Operation 1 (modify): Given two nodes $u, v$ on the chain and an integer $d$, add $d$ to the weight of every node on the unique simple path from $u$ to $v$ on the chain. Operation 2 (query): Given two positive integers $l, r$, compute the sum of node-weight sums over all simple paths whose number of nodes is at least $l$ and at most $r$. Since the answer can be very large, output the result modulo the prime $1000000007$. The node-weight sum of a simple path with $k$ nodes is the sum of the weights of all $k$ nodes (including endpoints) on that path. In this problem, you need to compute the sum of this value over all simple paths that meet the requirement. Since the graph is undirected, paths are undirected as well; that is, the path from node $1$ to node $2$ is the same as the path from node $2$ to node $1$, so do not double count.

The first line contains two positive integers $n, m$, denoting the number of nodes and the number of operations. The second line contains $n$ integers; the $i$-th number $a_i$ is the initial weight of the $i$-th node. Each of the next $m$ lines is in the form ```1 u v d``` or ```2 l r```, indicating an Operation 1 (modify) or Operation 2 (query), respectively.

For each query, output one line with one integer, which is the answer modulo $1000000007$.

### Sample Explanation: There is exactly $1$ simple path with $5$ nodes, and its node-weight sum is $5$, so the first query outputs $5$. There are $5$ simple paths with $1$ node, each with node-weight sum $1$; there are $4$ simple paths with $2$ nodes, each with node-weight sum $2$, so the second query outputs $13$. After adding $2$ to the weights of nodes $1$ and $2$, the $5$ simple paths with $1$ node have node-weight sums $3$, $3$, $1$, $1$, $1$, so the third query outputs $9$. 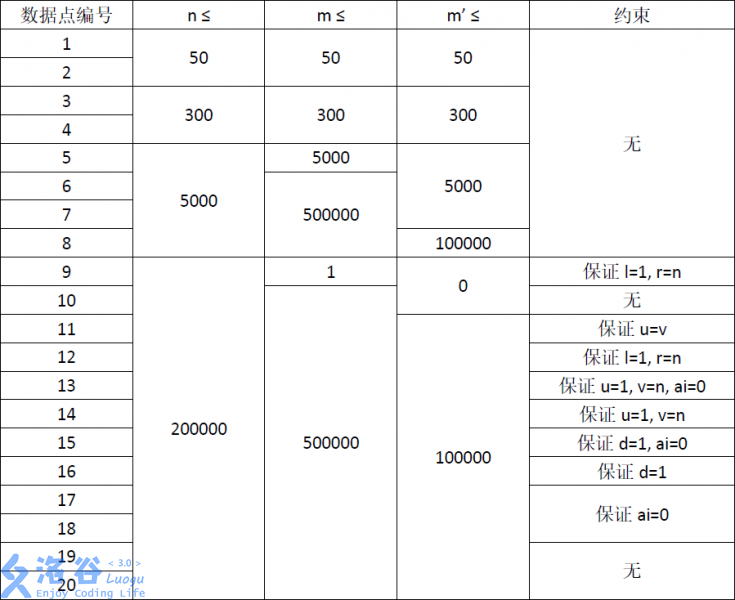### Constraints: Let the number of Operation 1 (modify) be $m^\prime$. For all testdata, it is guaranteed that $n \leq 200000$, $m \leq 500000$, $m^\prime \leq 100000$, $0 \leq a_i < 1000000007$. $1 \leq u \leq n$, $1 \leq v \leq n$, $0 \leq d < 1000000007$, $l \leq r \leq n$. For the detailed scale and conventions of each test point, see the table below.  Translated by ChatGPT 5