P4460 [CQOI2018] Unlock Screen
Background
Anyone who has used an Android phone should be familiar with gesture unlocking. Android’s lock screen consists of $3 \times 3$ points. By drawing a line on the screen to connect some of these points, you can form an unlock pattern. As shown in the three examples below:
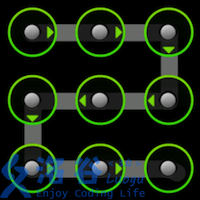
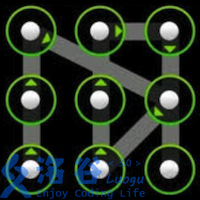
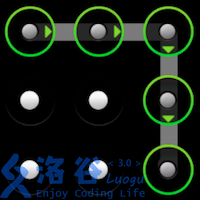
Description
When drawing the line, you must also follow some rules:
1. The number of connected points must be at least $4$. That is, connecting only two or three points will be considered invalid.
2. The segment between two points must be straight; it cannot bend.
3. Each point can be “used” at most once and cannot be repeated. Here, “use” means your finger passes over a point and it turns green.
4. A segment between two points cannot “pass over” another point, unless that point has already been “used” earlier.
For the last rule, see the explanation in the figure below. The two figures on the left violate the rule; the two on the right (namely $ 2 \rightarrow 4 \rightarrow 1 \rightarrow 3 \rightarrow 6$ and $ 6 \rightarrow 5 \rightarrow 4 \rightarrow 1 \rightarrow 9 \rightarrow 2$) do not violate the rule because, when “passing over” a point, that point has already been used.
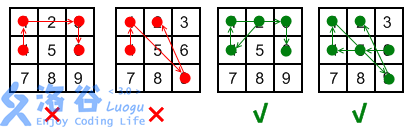
Now engineers want to improve the unlock screen by increasing or decreasing the number of points and moving their positions, so it is no longer a $3 \times 3$ grid, while keeping the drawing rules above unchanged.
Please compute how many line-drawing patterns on the new unlock screen satisfy the rules.
Input Format
The first line contains an integer $n$, the number of points.
The next $n$ lines each contain two space-separated integers $x_i$ and $y_i$, the coordinates of each point.
Output Format
Output a single line with the answer modulo $10^8+7$.
Explanation/Hint
#### Sample Explanation 1
Let the $4$ points be indexed $1$ to $4$. The valid patterns are $1 \rightarrow 2 \rightarrow 3 \rightarrow 4$, $2 \rightarrow 1 \rightarrow 3 \rightarrow 4$, $3 \rightarrow 2 \rightarrow 1 \rightarrow 4$, $2 \rightarrow 3 \rightarrow 1 \rightarrow 4$, and their mirror images.
### Constraints
- For $30\%$ of the testdata, $1 \le n \le 10$.
- For $100\%$ of the testdata, $-1000 \le x_i, y_i \le 1000$, $1 \le n < 20$. All point coordinates are distinct.
Translated by ChatGPT 5