P4468 [SCOI2007] Folding Paper

There is a square sheet of paper on the table with edges parallel to the coordinate axes. The lower-left corner is at $ (0, 0) $, and the upper-right corner is at $ (100, 100) $. Next, you will execute $n$ folding commands. Each command is specified by two distinct points $P_1(x_1, y_1)$ and $P_2(x_2, y_2)$. When executing a command, fold the current work along the line through $P_1P_2$, and fold the right side of the directed segment $ \overrightarrow{P_1P_2} $ toward the left side (the left side remains unchanged). After all folds, you need to punch a hole in the work and thread a string through it to hang it on the wall. The hole’s position is crucial: if it goes through too many layers of paper, punching the hole is difficult; if it goes through too few layers, the work may tear when hung. To choose a suitable hole position, you need to compute, for each candidate position, the number of layers the hole passes through. If the hole lies exactly on the boundary of a layer (within $0.000001$), that layer is not counted. This problem uses a simplified model: the paper has zero thickness, so each folding operation can be performed perfectly.

The first line contains an integer $n$, the number of folds. Each of the next $n$ lines contains four real numbers $x_1, y_1, x_2, y_2$, representing the directed segment used for that fold. The next line contains a positive integer $m$, the number of candidate positions. Each of the following $m$ lines contains two real numbers $x, y$, representing a candidate position.

For each candidate position, output one line containing an integer, which is the number of layers the hole passes through at that position.

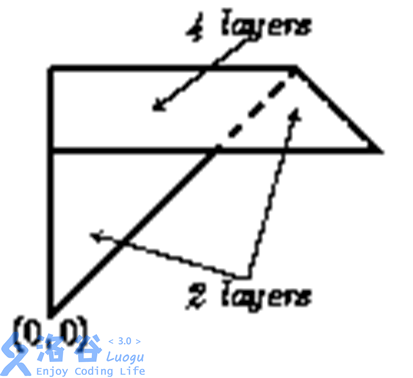
 Constraints: - $20\%$ of the testdata satisfy $n \le 1$. - $100\%$ of the testdata satisfy $0 \le n \le 8$, $1 \le m \le 50$. Translated by ChatGPT 5