P4487 [BJWC2018] Cross sum

First, let us introduce the game Kakuro (カックロ). The rules are: - Fill each empty cell with an integer from $1\sim 9$. - In a cell split by a diagonal line, the number in the upper-right corner equals the sum of the numbers in the consecutive adjacent cells to its right, and the number in the lower-left corner equals the sum of the numbers in the consecutive adjacent cells below it. - Whether horizontally or vertically, numbers in consecutive cells must not repeat.   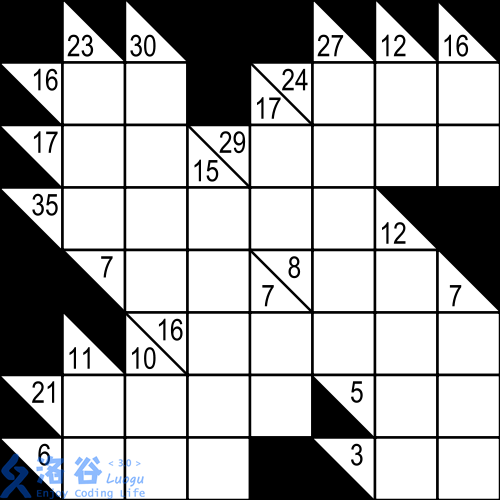The left picture shows a Kakuro puzzle, and the right picture shows its unique solution. We call the numbers given at the beginning clues, and the places that need to be filled are called empty cells. If a cell contains a clue, then it does not need to be filled. We guarantee that all puzzles are non-empty, meaning there is at least one empty cell that needs to be filled. **Note: The game rules in the following problems may be different. Please read the rules under each problem carefully.**

Game rules: - Fill each empty cell with a positive integer. - In a cell split by a diagonal line, the number in the upper-right corner equals the XOR sum of the numbers in the consecutive adjacent cells to its right, and the number in the lower-left corner equals the XOR sum of the numbers in the consecutive adjacent cells below it. - All integers filled in empty cells must be pairwise distinct (no duplicates). Apia gave Rimbaud a Kakuro puzzle. Rimbaud is not good at such puzzles at all, so she asks you to help solve it. Since Rimbaud is very young, she can only operate on numbers not exceeding $2^{60}-1$. Therefore, it is required that in the solution of the puzzle, every number does not exceed $2^{60}-1$.

Each input contains multiple test cases. The first line contains an integer $T$, the number of test cases. For each test case, the first line contains two positive integers $n, m$, representing the number of rows and columns of the board. In the next $n$ lines, each line contains $m$ digits from $0$ to $4$. The digit in row $i$, column $j$ indicates the type of the cell at $(i, j)$: - $0$ means this cell is neither an empty cell nor a clue cell. - $1$ means this cell contains a clue in the lower-left corner, and no clue in the upper-right corner. - $2$ means this cell contains a clue in the upper-right corner, and no clue in the lower-left corner. - $3$ means this cell contains clues in both the lower-left and upper-right corners. - $4$ means this cell is an empty cell. The input guarantees that, in terms of format, this is a valid Kakuro puzzle: for every consecutive segment of empty cells, the cell to its left or the cell above it contains a clue. Then there are $n$ more lines. Each line contains several **non-negative integers**, giving all clues in the puzzle in left-to-right order. In particular, if a cell type is $3$, then the lower-left clue is given first, followed by the upper-right clue.

For each test case, if there is a solution, output $n$ lines. Each line should output, from left to right, the numbers filled into the empty cells in that row. The filled numbers must be between $1$ and $2^{60}-1$ (inclusive). Otherwise, output $-1$.

For $10\%$ of the testdata, it is guaranteed that $n, m \leq 3$. For $30\%$ of the testdata, it is guaranteed that $n, m \leq 15$. For $50\%$ of the testdata, it is guaranteed that $n, m \leq 40$. For another $20\%$ of the testdata, it is guaranteed that only the cell at the first row and first column contains clues, and all remaining cells are empty cells. For $100\%$ of the testdata, it is guaranteed that $3 \leq n, m \leq 200$, $1 \leq T \leq 5$, and every initial clue number does not exceed $2^{60}-1$. Translated by ChatGPT 5