P4488 [BJWC2018] Kreuzsummen

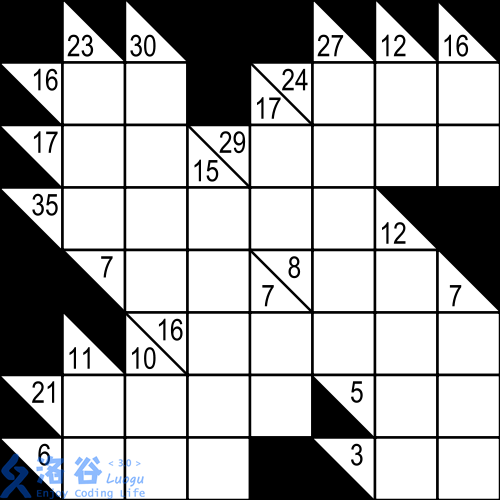
First, let’s introduce the game Kakuro (カックロ). Rules: - Fill each square cell with an integer from $1$ to $9$. - In a cell split by a diagonal slash, the number at the top-right equals the sum of the consecutive cells to its right, and the number at the bottom-left equals the sum of the consecutive cells below it. - In any horizontal or vertical run, digits may not repeat.   The left is a Kakuro puzzle, and the right is its unique solution. We call the numbers given at the start clues, and the places where numbers need to be filled empty cells. If a cell contains a clue, then no number needs to be filled there. We assume every puzzle is non-empty, i.e., at least one empty cell needs to be filled. Note: The game rules in the following problems may differ. Please read the rules under each problem carefully.

Rules: - Fill each square cell with an integer from $1$ to $k$. - In a cell split by a diagonal slash, the number at the top-right equals the sum of the consecutive cells to its right, and the number at the bottom-left equals the sum of the consecutive cells below it. - In any horizontal or vertical run, digits may not repeat. Apia gave Rimbaud a Kakuro puzzle. Clumsy as she is, Rimbaud keeps failing to solve Kakuro. She suspects the reason is that Apia’s puzzle is too hard rather than her own skill. So she wants to evaluate the difficulty of this puzzle. Rimbaud defines the difficulty of a Kakuro puzzle as the sum, over all empty cells, of the sizes of their candidate sets. For each empty cell, its candidate set is defined using only the initial puzzle’s row and column clues and the “no repetition” rule, considering the cell in its row and column runs independently. For example, if a run of $4$ consecutive cells has a clue sum $10$, then the four digits must be $1 + 2 + 3 + 4$. That is, under this clue, the candidate set for these cells is $\{1, 2, 3, 4\}$. More generally, if a run of $c$ consecutive cells has a clue sum $s$, consider all $c$-tuples of distinct numbers from $1$ to $k$ that sum to $s$. Under this clue, the candidate set for these cells is the set of all digits that appear in any of those $c$-tuples. For any given empty cell, its candidate set is the intersection of the candidate set from its row run and that from its column run.  In this puzzle, consider the empty cell at row $2$, column $2$. The row clue is $16$, giving a candidate set $\{7, 9\}$. The column clue is $23$, giving a candidate set $\{6, 8, 9\}$, so the cell’s candidate set is $\{9\}$. For the cell at row $2$, column $3$, the row clue gives $\{7, 9\}$ and the column clue gives $\{6, 7, 8, 9\}$, so the candidate set is $\{7, 9\}$. Note that although one could deduce more by first fixing row $2$, column $2$ and then using the row clue to determine row $2$, column $3$, Rimbaud only considers the initial clues. Please help Rimbaud compute the difficulty of this puzzle, i.e., the sum of the sizes of the candidate sets over all empty cells.

The first line contains four positive integers $n, m, k, T$, denoting the number of rows, columns, the value range, and the total number of clues. The next $T$ lines each contain five positive integers $t, x, y_1, y_2, s \ (t \in \{0, 1\},\ y_1 \le y_2)$. Here $t$ indicates the type of clue: - If $t = 0$, this is a row clue: in row $x$, columns $y_1$ to $y_2$ sum to $s$. - If $t = 1$, this is a column clue: in column $x$, rows $y_1$ to $y_2$ sum to $s$. Rows and columns are $1$-indexed. The empty cells of the puzzle are the union of all cells covered by the clues. The input is guaranteed to be a syntactically valid Kakuro puzzle: for every run of consecutive empty cells, the cell immediately to its left or above contains the corresponding clue, and each empty cell is covered by exactly two clues (one row clue and one column clue). The testdata may contain positions where the candidate set is empty or the puzzle is unsatisfiable. In such cases, still compute the difficulty strictly by the definition above.

Output a single integer, the answer.

// The following explains this sample. ``` -1 -1 -1 -1 -1 -1 -1 -1 -1 1 2 -1 -1 3 3 2 -1 2 2 -1 2 4 4 2 -1 3 4 1 2 5 -1 -1 -1 -1 1 5 -1 6 5 -1 -1 -1 -1 4 5 5 5 3 -1 8 8 5 6 -1 4 3 -1 2 3 3 -1 -1 2 2 ``` For $10\%$ of the testdata, it is guaranteed that $n, m \le 3$. For $30\%$ of the testdata, it is guaranteed that $n, m \le 50$. For $50\%$ of the testdata, it is guaranteed that $n, m \le 500$. For another $20\%$ of the testdata, only the cell at row $1$, column $1$ contains a clue, and all other cells are empty. For $100\%$ of the testdata, it is guaranteed that $3 \le n, m, T \le 10^5$, $1 \le k \le 10^5$, $s \le 10^{18}$. Translated by ChatGPT 5