P4492 [HAOI2018] Apple Tree

HAOI2018 Round2 Problem 1.

Xiao C planted an apple tree in his garden. Every node on the tree has exactly two branches. After careful observation, Xiao C found that each day the tree grows exactly one new node. On the first day, the tree grows a root node. On every subsequent day, the tree randomly chooses one branch in the current tree that has not yet produced a node, and grows a new node on that branch. The new node is connected by an edge to the node that the branch belongs to. Xiao C defines the “inconvenience” of an apple tree as the sum of distances between all pairs of nodes on the tree. The distance between two nodes is defined as the number of edges on the path from one to the other. He is very curious: if Xiao G comes to pick apples after $N$ days, what is the expected inconvenience $E$? However, Xiao C hates fractions, so he only wants to know the result of $E \times N !$ modulo $P$. It can be proven that this is an integer.

Read from standard input. A single line contains two integers $N$, $P$.

Print to standard output. Output a single integer representing the answer.

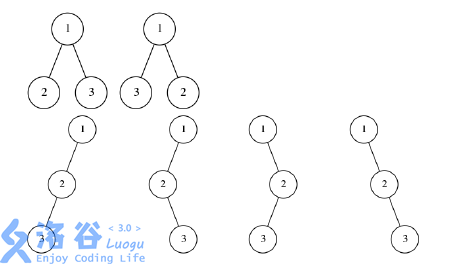
 The above shows all possible apple tree shapes when $N = 3$, where the label on each node indicates the day on which it grew. Clearly, in every case the sum of pairwise node distances is $4$. ### Constraints | Test point ID | $N$ | $P$ | | :--------: | :--: | :--: | | $1$ | $\le 10$ | $\le 10^9 + 7$ | | $2$ | $\le 10$ | $\le 10^9 + 7$ | | $3$ | $\le 500$ | $\le 10^9 + 7$ | | $4$ | $\le 500$ | $\le 10^9 + 7$ | | $5$ | $\le 500$ | $\le 10^9 + 7$ | | $6$ | $\le 2000$ | $= 10^9 + 7$ | | $7$ | $\le 2000$ | $= 10^9 + 7$ | | $8$ | $\le 2000$ | $\le 10^9 + 7$ | | $9$ | $\le 2000$ | $\le 10^9 + 7$ | | $10$ | $\le 2000$ | $\le 10^9 + 7$ | Translated by ChatGPT 5