P4493 [HAOI2018] Substring Coverage

Xiao C is quite into strings. He finds traditional string matching too boring, so he came up with the following problem. For two strings $A, B$ of length $n$, each time he gives four parameters $s, t, l, r$. Let $T$ be the substring of $A$ from $s$ to $t$ (1-indexed), and let $P$ be the substring of $B$ from $l$ to $r$. Then he performs the following operation: If some substring of $T$ equals $P$, we can cover this substring of $T$ and gain $K - i$, where $i$ is the starting position of this substring in $A$ at the beginning (note: not in $T$), and $K$ is a given parameter. A position cannot be covered more than once. The covering operation can be performed any number of times. You need to output the maximum total gain. Note that each query is independent, i.e., after finishing a query, the covered positions are restored.

The first line contains two integers $n, K$, denoting the string length and the parameter. The next line contains a string $A$. The next line contains a string $B$. The next line contains an integer $q$, denoting the number of queries. Each of the next $q$ lines contains four integers $s, t, l, r$, describing one query.

Output $q$ lines, each containing one integer, the answer for each query.

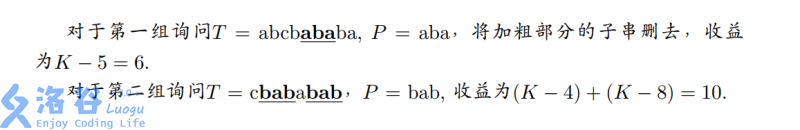
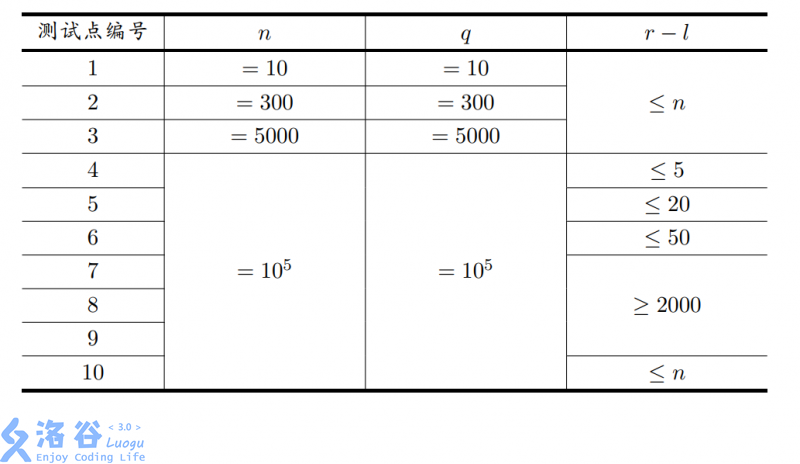
Explanation for Sample 1:  For all testdata, $1 \le n, q \le 10^5$, $A, B$ consist only of lowercase English letters, $1 \le s \le t \le n$, $1 \le l \le r \le n$, $n < K \le 10^9$. HAOI2018 Round 1 T3. For the testpoint with $n = 10^5$, the number of queries satisfying $51 \le r - l \le 2 \times 10^3$ does not exceed $11000$, and $l, r$ are uniformly random. Constraints  Translated by ChatGPT 5