P4494 [HAOI2018] 反色游戏
题目描述
小 C 和小 G 经常在一起研究搏弈论问题,有一天他们想到了这样一个游戏——
有一张 $n$ 个点 $m$ 条边的无向图,初始时每个节点有一个颜色,要么是黑色,要么是白色。
现在他们对于每条边做出一次抉择:要么将这条边连接的两个节点都反色(黑变白,白变黑),要么不作处理。
他们想把所有节点都变为白色,于是他们想知道在所有 $2^m$ 种可能的决策中,有多少种方案能达成这个目标。
然而,小 G 认为这个问题太水了,于是他还想知道,对于第 $i$ 个点,在删去这个点及与它相连的边后,新的答案是多少。
由于答案可能很大,你只需要输出答案对 $10^9+7$ 取模后的结果。
输入格式
第一行一个正整数 $T$,表示数据组数。
对于每组数据:
第一行两个整数 $n,m$ 表示图的点数和边数。
接下来 $m$ 行,每行两个整数 $u,v$,描述无向图的一条边 $(u,v)$。
接下来一行一个长度为 $n$ 的 01 串:
- 如果第 $i$ 个字符为 $\tt 0$,表示第 $i$ 个点为白色;
- 如果第 $i$ 个字符为 $\tt 1$,表示第 $i$ 个点为黑色。
输出格式
对于每组数据,输出一行 $n+1$ 个整数:
第一个整数表示不删去任何点时的答案(输出后不要换行);
接下来 $n$ 个整数,第 $i$ 个表示删去第 $i$ 个点时的答案。
答案对 $10^9+7$ 取模。
说明/提示
对于所有数据,有 $1\le T\le l0^5,1\le n,m\le10^5,1\le u,v\le n$,且给定的无向图没有重边和自环。
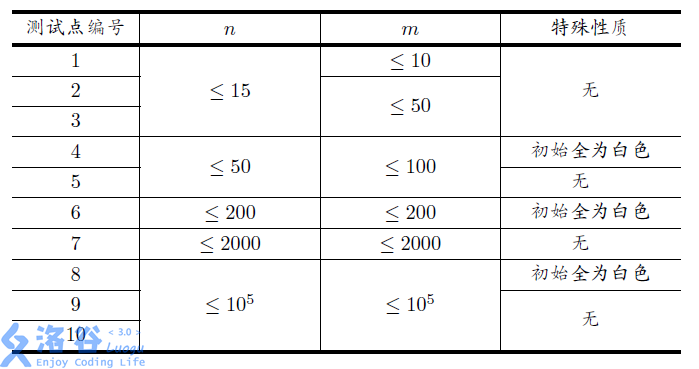
*[Source: HAOI2018 Day 1 T2]*