P4499 [CTSC2011] Bridges of the Infinite Graph

The goal is to find all bridges in an undirected graph with infinitely many nodes. This undirected graph has the following properties: 1. The graph is connected. 2. All nodes are partitioned into infinitely many layers: layer $1$, layer $2$, layer $3$, $\cdots$, with $n$ nodes in each layer. For convenience, we denote the $x$-th node in layer $i$ by $(i, x)$. 3. Edges are allowed between nodes within the same layer, and between nodes in adjacent layers. No other edges are allowed. 4. If there is an edge of weight $d$ between $(i, x)$ and $(i, y)$, then for any positive integer $j$, there is also an edge between $(j, x)$ and $(j, y)$ with weight $0.9^{j-i} d$, where $j$ is any positive integer. 5. If there is an edge of weight $d$ between $(i, x)$ and $(i + 1, y)$, then for any positive integer $j$, there is also an edge between $(j, x)$ and $(j + 1, y)$ with weight $0.9^{j-i} d$, where $j$ is any positive integer. The undirected graph shown below satisfies all the properties above. An undirected graph with infinitely many nodes is connected if and only if there exists a path between any pair of nodes in the graph. An edge is a bridge if and only if removing it makes the entire graph disconnected.  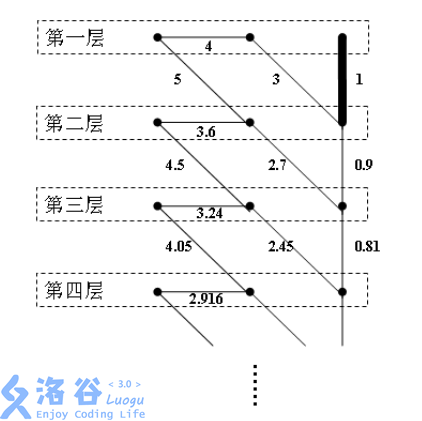Please write a program to read this connected infinite graph and compute the sum of weights of all its bridges. For example, in the figure above, the bold edge is the unique bridge, so the sum of weights of bridges is $1$.

The input file infinite.in contains three space-separated non-negative integers on the first line: $n$, $m_1$, and $m_2$. From line $2$ to line $m_1 + 1$, each line contains three positive integers $x$, $y$, and $d$, indicating that there is an edge of weight $d$ between $(1, x)$ and $(1, y)$. From line $m_1 + 2$ to line $m_1 + m_2 + 1$, each line contains three positive integers $x$, $y$, and $d$, indicating that there is an edge of weight $d$ between $(1, x)$ and $(2, y)$. Each line’s three integers are separated by a single space. There may be more than one edge between nodes $x$ and $y$. Self-loops are allowed.

The output file infinite.out contains exactly one line with a real number: the sum of weights of all bridges, rounded to two decimal places.

[Sample Explanation 1] This is the same as the example given in the problem statement. Constraints ||||| | :----------- | :----------- | :----------- | :----------- | | Data ID | $n$ | $m_1$ | $m_2$ | | 1 | $\leq 10$ | $\leq 50$ | $\leq 50$ | | 2 | $\leq 10000$ | $\leq 40000$ | $\leq 40000$ | | 3 | $\leq 300000$ | $\leq 500000$ | $=1$ | | 4~7 | $\leq 300000$ | $\leq 500000$ | $\leq 500$ | | 8~10 | $\leq 300000$ | $\leq 500000$ | $\leq 500000$ | In 100% of the testdata, $d \leq 100$. Translated by ChatGPT 5