P4500 [ZJOI2018] Tree

Jiutiao Kelian (pinyin) is a girl who loves to write problems. Although writing problems itself is very interesting, turning a problem into an official contest task is not so fun: generating testdata is always exhausting. In ZJOI 2018 Day 1, Kelian set a very interesting problem about trees. She plans to use a common method to randomly generate a rooted tree with $n$ nodes: - Node $1$ is the root of the tree. - For $i \in [2, n]$, independently and uniformly at random pick a node from $[1, i)$ as the parent of $i$. Kelian does not really want to think about whether such randomly generated testdata can defeat brute force, since hacking around is also part of OI contests. What Kelian cares about more is the problem's discriminative power, and whether all possible scores appear. Therefore, she hopes that the trees in any two test points are different, so that an incorrect program might pass only one of them. Thus, Kelian wants to compute the probability that, by independently generating $k$ rooted trees with $n$ nodes $T_1$ to $T_k$ using the method above, they are pairwise isomorphic. Two rooted trees $T_1$ and $T_2$ with $n$ nodes are isomorphic if and only if there exists a permutation $p$ of length $n$, satisfying $p_1 = 1$, and for all $i \in [2, n]$, if the parent of $i$ in $T_1$ is $f$, then the parent of $p_i$ in $T_2$ is $p_f$.

The first line contains three integers $n, k, p$, denoting the number of nodes, the number of trees, and the modulus. It is guaranteed that $10^8 \leq p \leq 10^9$ and $p$ is prime.

Output a single integer, the answer modulo $p$. That is, if the answer in lowest terms is $\frac{a}{b}$, output $a \times b ^{-1} \bmod p$.

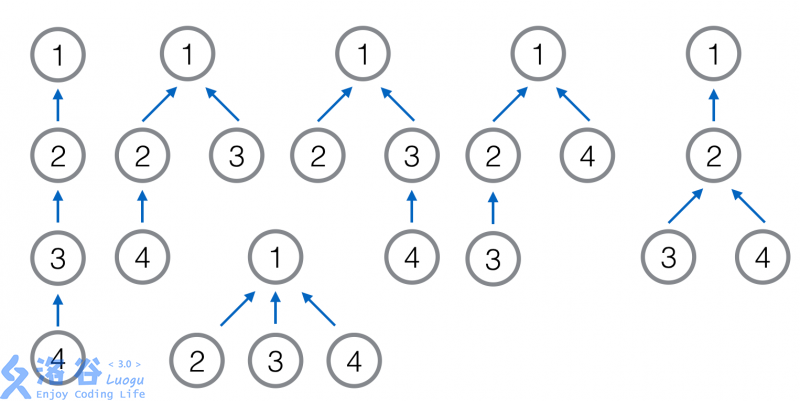
Sample Explanation In the first sample, the generated tree is unique, so the two generated trees are necessarily identical. In the second sample, there are only two possible generated trees, and they are non-isomorphic. Therefore, the probability that the two generated trees are isomorphic is $\frac{1}{2}$, which is $499122177$ modulo $998244353$. In the third sample, there are $6$ possible generated trees, as shown below. Among them, the second, third, and fourth (the middle three in the first row) are isomorphic, and the remaining ones are pairwise non-isomorphic. Therefore, the probability that the two generated trees are isomorphic is $\frac{1}{3}$, which is $332748118$ modulo $998244353$.  Constraints 测试点| $n$| $k$|测试点| $n$| $k$ -|-|-|-|-|- 1|$\le 5$|$=2$|6|$\le 50$|$\le 10^9$ 2|$\le 10$|$=2$|7|$\le 200$|$\le 10^9$ 3|$\le 20$|$=2$|8|$\le 500$|$\le 10^9$ 4|$\le 50$|$=2$|9|$\le 1000$|$\le 10^9$ 5|$\le 50$|$=2$|10|$\le 2000$|$\le 10^9$ For $100\%$ of the testdata, it is guaranteed that $p$ is prime and $10^8 \le p \le 10^9$. Thanks to @Xeonacid for providing the statement. Translated by ChatGPT 5